Antes de apresentar o Teorema de
Bayes, convém relembrar a definição de probabilidade condicional, para destacar
a diferença entre este conceito e o próprio teorema.
❗ Definição
A probabilidade condicional de um evento B dado que ocorreu o evento A é a chance de ocorrer B sob a condição de que A tenha ocorrido. Representa-se por P(B∣A), que se lê: “probabilidade de B dado A”.
É importante observar que:
🔸 A e B são eventos dependentes.
🔸 O evento A ocorre antes do evento B.
🛑 Exemplo
Uma urna contém cinco bolas que se diferenciam apenas pela cor: duas
vermelhas e três azuis. Retiram-se duas bolas sem reposição, uma após a
outra.
Pergunta: Qual a
probabilidade de a segunda bola ser vermelha, sabendo que a primeira
era azul?
Um diagrama de árvore ajuda a visualizar os
possíveis desfechos nessa situação. Todas as probabilidades condicionais são
indicadas, e a resposta à pergunta está destacada em amarelo.
A resposta é dada pela regra da multiplicação de
probabilidades para eventos dependentes:
❗ TEOREMA DE BAYES
⚠️P
1. Seja A: “ter treinamento técnico”. Seja B:
“executar um bom serviço”.
🔸 P(B∣A): probabilidade de executar um bom serviço dado
que tem treinamento técnico.
🔸 P(A∣B): probabilidade de ter treinamento técnico dado
que executou um bom serviço.
2. Seja A: “ter sido bom aluno no colegial”. Seja B:
“ter sido aprovado no vestibular”.
🔸 P(B∣A): probabilidade de aprovação no vestibular dado
que foi bom aluno.
🔸 P(A∣B): probabilidade de ter sido bom aluno dado que
foi aprovado no vestibular.
Esses pares de probabilidades aparecem
frequentemente em problemas reais. Vamos buscar agora uma fórmula para
calcular P(A∣B).
Igualando as expressões:
🛑 Exemplo
– Aplicando o Teorema de Bayes
Vamos
voltar ao exemplo das bolas da urna, agora com uma pergunta
diferente:
Pergunta: Qual é a probabilidade de a primeira bola retirada ter sido uma bola azul,
sabendo que a segunda era vermelha?
Pelo
diagrama de árvore, vemos que a segunda bola ser vermelha pode ocorrer de duas
maneiras:
· Azul e vermelha (A-Z)
· Vermelha e vermelha (V-V)
O evento de interesse é: primeira azul dado segunda vermelha, isto é:
Teorema de Bayes: Sejam A e B dois eventos dependentes que ocorrem em sequência, A antes de B. A probabilidade de ocorrer A sob a condição de B ter ocorrido é dada por:
Observe o
esquema abaixo: está marcado o evento de interesse, que é a probabilidade de
ocorrer A dado que B tenha ocorrido. Mas B pode ocorrer de duas maneiras: depois de A
e depois de A -traço.
🔔 Interpretação
O Teorema de Bayes inverte a ordem da
informação:
· A probabilidade
condicional trata de P
· O Teorema de
Bayes trata de P
🛑 Exemplo – Teste do bafômetro
Em
uma cidade, o teste do bafômetro é obrigatório.
· 25% dos motoristas bebem antes de
dirigir.
· Dos que bebem, 99% testam positivo.
· Dos que não
bebem, 17% também testam positivo.
Pergunta: Se um motorista testou positivo,
qual a chance de ele ter realmente ingerido bebida alcoólica?
Use os eventos: B
A probabilidade pedida é:
Dois
cavalos correm: Branco e Negro.
· Em 12 corridas anteriores, Branco
venceu 5 vezes e Negro 7.
· Em 3 das 5 vitórias de Branco, chovia.
· Em 1 das 7 vitórias do Negro, também
chovia.
Está chovendo agora. Qual a probabilidade de Branco
vencer?
O
que queremos é:
Use os dados no diagrama de árvore
para encontrar a probabilidade:
**************************

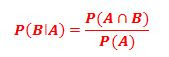














10 comments:
Espectacular explicação do teorema de Bayes. Parabéns!!!!
O resposta da urna não é 3/10 ?
Amei a explicação!!!
Obrigada, João, pela dica.Acho que agora está bem.
a pergunta sobre o exercício do bafômetro esta meio equivocado, acho q a pergunta n coincide com a resposta dada, a resposta da pergunta ja esta no desenho do diagrama. "qual a probabilidade de dar positivo sendo que ele nao bebeu" e a probabilidade disso esta no diagrama
Tem razão, Caroline, a questão estava incorreta. Obrigada.
Parabéns pela ótima explicação. Isto me ajudou muito. Seu talento é muito raro pois pouquíssimas pessoas conseguem explicar algo complexo tão facilmente.
Obrigada, é o ofício de professora que, para mim, demanda mais transpiração do que inspiração.
Acho q o evento de interesse é as pessoas que não bebem e positivarem o bafômetro, nesse caso colocar 0,1275 no nominador, do modo que fique: 0,1275/ 0,3750 = 34%, faz sentido?
Post a Comment