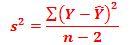Regressão linear simples I

Regressão linear simples é um método estatístico que permite estudar a relação entre duas variáveis quantitativas, que chamaremos de X e Y.

X é a variável explicativa ou independente.

Y é a variável resposta ou dependente.

A regressão linear simples recebe o nome de “simples” porque trabalha como uma só variável explicativa. Quando a variável resposta é função de duas ou mais variáveis explicativas, a regressão linear é múltipla.

                                                             EXEMPLOS

1.    Dados peso e altura de pessoas adultas, você pode pensar em uma regressão linear simples que coloque peso como função da variável  altura. Então peso é a variável dependente e altura a variável independente.

2.    Dados peso e altura de pessoas com 6 a 10 anos de idade, você pode pensar em uma regressão linear múltipla que coloque peso com variável resposta (ou dependente) de duas variáveis explicativas (ou independente): idade e altura.Em outras palavras, o peso de uma criança depende da idade e da altura.

     RELAÇÕES DETERMINÍSTICAS E RELAÇÕES PROBABILÍSTICAS

   Antes de continuar, é preciso lembrar que duas variáveis, X e Y, podem ter uma relação determinística, ou seja, matemática, como é a relação entre graus Fahrenheit e graus Celsius:

Quando colocados em diagrama de dispersão, os pontos caem exatamente sobre uma reta, como mostra a Figura 1. Isto acontece porque a equação da reta é a descrição exata da relação entre as duas variáveis.

Figura 1

Diagrama de dispersão: pontos sobre uma reta

   Vamos estudar aqui a relação estatística entre uma variável resposta Y e uma variável explicativa X. Para começo de conversa, imagine que o fenômeno que você está estudando é bem descrito por uma reta porque, quando coloca os dados empíricos em um diagrama de dispersão, os pontos formam uma “nuvem” em torno de uma reta. Mas nessa “nuvem” caberia uma infinidade de retas. Veja a Figura 2, em que X poderia ser, por exemplo, a altura de pessoas e Y seria o peso. É preciso traçar, então, a reta que melhor se ajusta aos dados. A questão é: qual é a melhor reta?

Figura 2

Diagrama de dispersão: pontos em torno de uma reta

     É preciso estabelecer um critério para determinar a melhor reta, mas qualquer que seja a reta será sempre apenas uma aproximação para o verdadeiro fenômeno: não há como fazer previsões exatas com base em dados empíricos. E temos que nos haver com a questão estatística de estimação dos parâmetros porque a reta será ajustada usando os dados de uma amostra e não de toda a população. Quais são esses parâmetros, quando se fala em uma reta?

       A equação de uma reta é dada por

Y = a + b X,

     Nessa equação, a é o intercepto porque é o valor que Y assume quando X = 0, ou seja, quando a reta corta (intercepta) o eixo das ordenadas; b é uma medida da inclinação da reta. Não é preciso saber mais do que isto para entender a equação de uma reta, mas não custa lembrar você de que b  é a tangente trigonométrica do ângulo q  delimitado pela reta de equação Y = a + bX e pela reta paralela ao eixo das abscissas que passa pelo ponto a. Veja a Figura 3.

     Quando Y é uma variável aleatória, você pode descrever Y em função de X com o modelo:

                                               Y = a + b X + e,

    Nesse modelo,  a e b  são parâmetros e e  é o erro aleatório. Para entender o que é o erro aleatório, observe a Figura 3: e   é a distância entre a resposta de uma observação e a reta de regressão para toda a população.

Figura 3

O erro aleatório

    Se você tem dados de uma amostra, pode obter os valores a e b que estimam os parâmetros a e b  da reta. Mas para ajustar uma regressão linear simples a um conjunto de dados, é necessário fazer algumas pressuposições.

                           PRESSUPOSIÇÕES BÁSICAS

  Pressuposição 1: A relação entre as duas variáveis é linear.

Você só deve traçar uma reta para descrever um fenômeno se, no intervalo estudado, a relação entre as duas variáveis é expressa por uma reta. Para saber se a reta é, de fato, o modelo adequado para que descrever o fenômeno, existem dois procedimentos: ou você conhece a teoria que diz que o fenômeno é linear ou você “vê a relação linear”, olhando o gráfico.

Pressuposição 2: A variabilidade de Y, para qualquer valor dado de X, é sempre a mesma.

A variabilidade é medida pela variância. Então esta pressuposição estabelece que a variância de Y é constante, qualquer que seja o valor de X. 

Pressuposição 3: O erro de uma observação não está correlacionado com o erro de outra observação.

As observações devem ser independentes. O que isto significa? Por exemplo, fazer a mesma pergunta 20 vezes para uma única pessoa não é igual a fazer a mesma pergunta para 20 pessoas diferentes. No primeiro caso, as respostas não são independentes: uma pessoa responde da mesma maneira (ou de maneira similar) a perguntas iguais. No segundo caso, é razoável supor que as respostas sejam independentes, desde que as pessoas tenham sido retiradas ao acaso da mesma população ( enão de um grupo fechado).

Pressuposição 4: Para qualquer valor de X, os valores de Y têm distribuição normal.

Para qualquer valor de X, os valores de Y têm distribuição normal ou, o que é o mesmo, os desvios (Y – Ŷ) têm distribuição normal. Mas esta pressuposição  só é essencial para proceder aos testes estatísticos. Os programas estatísticos geralmente fazem uma análise dos resíduos. Algumas dessas análises são gráficas e constituem a maneira fácil de visualizar se os desvios fogem muito da pressuposição de normalidade.

Pressuposição 5: Os valores de X são fixos, isto é, X não é variável aleatória.

Cabe, aqui, um comentário: essa pressuposição não é, na realidade, essencial. Em certas condições, mesmo que X seja uma variável aleatória, pode ser ajustada uma reta aos pares de valores X e Y.

Estimativas dos parâmetros

    Para obter a e b, você aplica as fórmulas dadas em seguida ou, melhor ainda, faz os cálculos usando um computador. A dedução dessas fórmulas será apresentada em nova postagem. As fórmulas são:

EXEMPLO

Este exemplo é do tutorial do SPSS: 

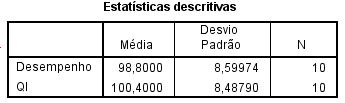
Uma empresa quer saber se é possível medir o desempenho no trabalho a partir de escores de QI. A empresa então faz medidas desempenho no trabalho e QI em 10 funcionários. Veja os dados apresentados na Tabela 1.

Tabela 1

Dados de QI e desempenho de dez funcionários

Para obter os valores de a e b, os cálculos intermediários estão apresentados na Tabela 2.

Tabela 2

Cálculos intermediários para obtenção de a e b

Para obter o valor de b, é preciso calcular:

    Para obter o valor de a, é preciso calcular as médias de X e de Y:

    Então:

    Obtidos os valores de a e b, pode-se escrever a equação da reta:

    Agora, é fácil traçar a reta no gráfico. Basta dar dois valores quaisquer para X (como zero e 5) e calcular os valores de Y. Para X = 0, tem-se que:

    Para X=5:

    De posse de dois pares de valores de X e Y, é possível construir o gráfico apresentado na Figura 4.

Figura 4

 Reta de regressão 

Variâncias dos parâmetros

    Para obter V(b) e V(a), você aplica as fórmulas dadas em seguida ou, melhor ainda, faz os cálculos usando um computador. As fórmulas, lembrando que s² é um parâmetro, são:

    A questão é obter uma estimativa de s². Sem aplicar uma análise de variância, que veremos em nova postagem, você calcula, para o exemplo que estamos desenvolvendo, a estimativa de s²:

    A Tabela 3 apresenta os cálculos intermediários para obter s². Lembre-se de que os valores estimados da reta são dados por

Tabela 3

Cálculos intermediários para obtenção de s²

    Você obtém o erro padrão de a e de b extraindo a raiz quadrada das respectivas variâncias. Para o exemplo:

     Para testar as hipóteses de que os parâmetros a e b são iguais a zero, contra as alternativas de que são diferentes de zero, aplique o teste t ao nível de significância desejado:

    Compare os valores calculados de t com os valores da distribuição de t com n-2 graus de liberdade e ao nível de significância estabelecido.

Para o exemplo que estamos desenvolvendo:

    No nível de 5% de significância e com n-2=8 graus de liberdade, t = 2,306. Logo, a hipótese de que b = 0 deve ser rejeitada.

    Você pode, também, obter os intervalos de confiança para os parâmetros a e b. Sendo t₀ o valor crítico de t com n-2 graus de liberdade e ao nível escolhido de significância, você ontem os intervalos como segue: 

        Para o exemplo:

Se você usar o SPSS, vai obter, para o que foi visto aqui:

VEJA REGRESSÃO LINEAR PASSANDO PELA ORIGEM EM OUTRA POSTAGEM.

Kolmogorov- Smirnov : teste de normalidade

Aplicamos o teste de aderência de Kolmogorov-Smirnov para verificar se determinada amostra vem de população com distribuição específica. Essa “distribuição específica” é, na maioria das vezes, a distribuição normal. Nesses casos, podemos dizer que estamos usando o teste de normalidade de Kolmogorov-Smirnov.

Vamos ver, por meio de um exemplo, o procedimento para testar a hipótese de que erros em torno da média têm distribuição normal, usando o teste de normalidade de Kolmogorov-Smirnov.

EXEMPLO

Com um cronômetro na mão para medir o período de oscilação de um pêndulo, você faz n=20 medições. Os resultados estão na Tabela 1.

                                               Tabela 1

           Leituras do período de oscilação de um pêndulo, em segundos

A média aritmética das n=20 medidas é a melhor estimativa para o período de oscilação:

Os desvios da média, apresentados na Tabela 2, estimam os erros de medida. 

Tabela 2

Desvios da média das leituras do período

 de oscilação de um pêndulo, em segundos

A média dos desvios é

Como a média é igual a zero, o desvio padrão é dado por

Podemos organizar os dados na Tabela 3, de distribuição de frequências, e desenhar o histograma apresentado na Figura 1.

Tabela 3

Tabela de distribuição de frequências

Figura 1

Histograma para os desvios da média das leituras do período

 de oscilação de um pêndulo, em segundos

Podemos desenhar, sobre o histograma, a distribuição normal, com a mesma média e desvio padrão dos desvios apresentados na Tabela 2. Veja a Figura 2. 

                                                    Figura 2

                 Distribuição normal desenhada sobre o histograma

  Para aplicar o teste de Kolmogorov-Smirnov:

1.    As frequências acumuladas (FA_i) dos desvios.

2.   As frequências relativas  acumuladas (FRA_i) dos desvios.

3.    O valor padronizado (ou estandartizado) z_i para cada desvio d_i. A média será sempre zero mas, para o exemplo que estamos desenvolvendo, o desvio padrão calculado é s= 0,1487. Então, no exemplo:

4. As probabilidades acumuladas P_i  dos desvios padronizados sob a distribuição normal padronizada. Veja a Figura 3, em que a probabilidade acumulada até -1 está em cinza azulado.

Figura 3

Probabilidade acumulada sob a distribuição normal padronizada 

5. Os valores absolutos das diferenças D_i entre as frequências relativas acumuladas dos desvios FRA_i e as probabilidades acumuladas P_i  dos desvios.

6. Os valores absolutos das diferenças D_i’ entre as probabilidades acumuladas P_i dos desvios e as frequências relativas acumuladas dos desvios de uma classe imediatamente anterior FRA_i.

7.  Compare a maior estatística D_i ou D_i’ observada com o valor de D obtido em uma tabela de valores críticos de D para o teste de aderência de Kolmogorov-Smirnov para dados contínuos. A estatística de teste é:

8.   Rejeite a hipótese de que os desvios têm distribuição normal (a hipótese de nulidade) se a estatística D calculada for maior que a crítica dada na Tabela 5, ao nível estabelecido de significância e para o tamanho de amostra[1]. Veja os resultados desses cálculos na Tabela 4.

Tabela 4 

Cálculos auxiliares para o teste de aderência de Kolmogorov Smirnov

    O valor máximo encontrado para D foi 0,150, menor que o valor crítico para o nível de significância de 5%, com tamanho de amostra 20. Então não se rejeita a hipótese de que a distribuição é normal.

 Tabela 5

           Fonte: ZAR,J. Biostatistical Analysis. 4 ed. Prentice Hall. 1994.
Veja o resultado obtido pelo teste, feito no programa SPSS: não se rejeita a hipótese de normalidade. 

É bastante comum, quando se pretende aplicar uma análise de variância (ANOVA) aos dados experimentalmente, que se faça a pressuposição de que os erros são variáveis aleatórias independentes com distribuição normal. Veja um exemplo.

EXEMPLO

Todo produtor de milho quer ter maior produtividade. Imagine que um produtor colocou à disposição de um agrônomo uma área onde é possível alocar 20 parcelas para a experimentação de três híbridos além do que chamaremos testemunha, ou seja, o que o produtor planta em sua propriedade. A Tabela 6 apresenta os dados segundo o tratamento e, no rodapé, as médias. Até que ponto as diferenças observadas entre as médias dos tratamentos são suficientemente grandes para serem tomadas como evidência de que há diferença significante entre eles? A resposta para essa pergunta é dada por uma análise de variância, que testa a hipótese de que as médias populacionais são iguais, isto é:

contra a hipótese alternativa de que existe pelo menos uma média diferente das demais. 

Tabela 6

 Produtividade de milho em kg/100 m² segundo o tratamento

Teste a hipótese de que os erros têm distribuição normal. A média geral dos desvios é zero e o desvio padrão é 2,4279.

Outros testes de normalidade

Há vários testes de aderência à distribuição normal. Alguns deles, como o de Anderson- Darling e o de Kramer-von Mises são, na realidade, melhoramentos feitos sobre o teste de Kolmogorov- Smirnov[1]. Como são mais poderosos, são preferidos por muitos analistas.

     O teste de Shapiro-Wilk, proposto em 1965, tem se saído muito bem nos estudos de comparação com outros testes de aderência. Usa uma estatística complicada, que não será dada aqui. Para bem entender a estatística de teste, veja o trabalho original[2]. Mas é comum nos programas de computador e deve ser preferido quando a amostra é pequena. Veja o resultado obtido no teste de Shapiro-Wilk no exemplo anterior. E não se impressione com a diferença entre os valores p: as estatísticas de teste são diferentes. Além disso, o teste de Shapiro-Wilk tem mais poder (rejeita H₀ mais vezes).

---

[1] Kolmogorov-Smirnov Goodness-of-Fit Test. https://www.itl.nist.gov/div898/handbook/eda/.../eda35g.htm

[2]The Shapiro-Wilk and related tests for normality. https://math.mit.edu/~rmd/465/shapiro.pdf

---