Para
bem entender o teorema da soma de probabilidades, ajuda dividir a questão em
duas regras:
· regra nº 1, para soma de eventos mutuamente
exclusivos;
· regra nº 2, para soma de eventos não
mutuamente exclusivos.
Dois eventos são mutuamente exclusivos quando não podem ocorrer ao mesmo tempo.
Quando um dado é lançado, só pode ocorrer uma das faces. Se a ocorreu a face “cinco”, ficou excluída a possibilidade de ter ocorrido qualquer outra face.
Regra 1 da soma
(para eventos mutuamente exclusivos)
Se A e B são eventos mutuamente exclusivos, a probabilidade de ocorrer A ou B é igual à soma das probabilidades de ocorrer cada um deles. Escreve-se:
Quando você joga um dado, só pode ocorrer uma das faces. Qual é a probabilidade de, em um lançamento, ocorrer 1 ou 6? Usando a regra 1 da soma, você calcula a probabilidade de ocorrer 1 e a probabilidade de ocorrer 6. Depois, soma essas probabilidades.
Exemplo
Imagine um pote de vidro com 11 bolinhas de diferentes cores: 3 azuis, 4 brancas, 2 vermelhas, 1 amarela, 1 verde. Qual é a probabilidade de, em uma só retirada, ocorrer bola verde ou bola amarela? Usando a regra 1 da soma, você calcula a probabilidade de ocorrer bola verde e a probabilidade de ocorrer bola amarela. Depois, soma essas probabilidades.
Dois eventos A e B são não mutuamente exclusivos se eles têm pelo menos um resultado em comum.
Exemplo
Quando você joga um dado, só pode ocorrer uma das faces. Mas pense nos eventos: ocorrer “número ímpar” ou ocorrer “número maior do que quatro”. Esses dois eventos têm um resultado em comum: é o número cinco, que tanto pertence ao evento “número ímpar” como ao evento “número maior do que quatro”.
Veja a figura: “números ímpares” estão circundados por uma elipse azul e “números maiores do que quatro” por um retângulo vermelho. Se você contar o número de resultados que correspondem ao evento “número ímpar” e o número de resultados que correspondem ao evento “número maior do que quatro”, terá contado 5 duas vezes.
Se A e B são dois eventos não mutuamente exclusivos, há uma sobreposição, isto é, existe pelo menos um resultado de A que também é resultado de B. Então a probabilidade de ocorrer A ou B é dada pela probabilidade de A, mais a probabilidade de B, menos a probabilidade de A e B (que foi contada duas vezes). Escreve-se:
Exemplo
Quando você joga um dado, só pode ocorrer uma das seis faces. Qual é a probabilidade de, em um lançamento, ocorrer “número ímpar” ou ocorrer “número maior do que quatro”? Usando a regra 2 da soma, calcule a probabilidade de ocorrer “número ímpar”, a probabilidade de ocorrer “número maior que quatro” e probabilidade de ocorrer “número ímpar maior do que quatro”. Depois, aplique a regra 
Exemplo
Uma carta será retirada ao acaso de um baralho. Qual é a probabilidade de sair
um rei ou uma carta de copas?
Como um baralho tem 52 cartas,
das quais quatro são reis e 13 são de copas, alguém poderia pensar que a
probabilidade de sair um rei ou uma carta de copas é dada pela soma das probabilidades de sair um rei e de sair uma carta de espadas. Mas esta resposta está errada porque o rei de copas é tanto rei como copas. Então o rei de copas teria sido contado duas vezes – como rei e como copas. 
Exercícios
1. É dado o conjunto de dados: A={1; 2; 3; 4; 5; 6; 7; 8; 9; 10}.
a) Qual é a probabilidade de, ao se tomar um número ao
acaso desse conjunto A de dados, o número ser um ímpar menor do que 4 ou um
ímpar maior do que 8?
b) Qual é a probabilidade de, ao se
tomar um número ao acaso desse conjunto A de dados, o número ser um ímpar
ou múltiplo de 3?
2. Qual é a probabilidade de, ao lançar um dado, sair
número ímpar ou múltiplo de 3?
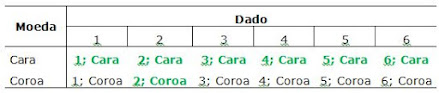
3. Jogam-se um dado e uma moeda. O jogador ganha se sair “cara” na moeda ou “2” no dado. Qual é a probabilidade de o jogador ganhar arremessando juntos o dado e a moeda?
Respostas
1. a) 3/10.
1. b) 3/5.
2. 2/3
3. 7/12
Como se chega a essas
respostas?
1.a) São 10 eventos possíveis. São eventos de interesse: ímpares menores do que
4, isto é, 1 e 3 e maiores do que 8, ou seja, só o 9. Veja os eventos de
interesse em vermelho:
1; 2; 3; 4; 5; 6; 7; 8; 9; 10.
Daí, a resposta 3/10.
1.b) São 10 eventos possíveis. São eventos de interesse: ímpares ou
múltiplos de 3. São ímpares: 1; 3; 5; 7; 9. São múltiplos de 3: 3; 6; 9.
Veja que os números 3 e 9 foram contados duas vezes, porque são tanto números
ímpares como múltiplos de 3. Usando a regra 2 da soma:
Veja as respostas de interesse marcadas em vermelho (ímpares) e circundadas por quadrado (múltiplos de 3):
2. São 6 eventos possíveis, dos quais 3 são números ímpares e 2 são múltiplos de 3, mas 3 é tanto ímpar como múltiplo de 3. Então, aplicando a regra 2 da soma:
Marcadas em vermelho, múltiplos de 3 e, em azul, os
ímpares.
3. Veja: tanto
faz sair “cara” na moeda ou “2” no dado, o jogador ganha nos dois casos. A
probabilidade de sair “cara” na moeda é
A
probabilidade de sair “2” no dado é
No entanto, pode “sair cara” na moeda e “2” no dado em uma única jogada. A probabilidade desse evento é
Logo, para calcular a probabilidade de o jogador ganhar, use a regra 2 da
soma. A probabilidade pedida é
Veja também
a tabela e conte: são 12 eventos possíveis; 7 são de interesse. Logo, a
probabilidade pedida é 7/12.










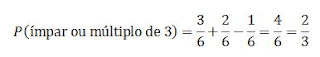

16 comments:
Que ótima explicação! Transformou em algo super simples de se entender. Utilizarei esses exemplos em aula. Obrigada
quando as bases são diferentes, vai mudar alguma coisa?
Ex:Um dado e uma moeda são lançados, qual a probabilidade de se obter uma coroa e um dois: Coroa:1/2 Dado:1/6. Tenho dúvidas sobre a base debaixo, haverá fatoração para igualar a base ou apenas vou somar?
Qual é a probabilidade de coroa na moeda e 2 no dado? Regra do e, ou seja, teorema da multiplicação: 1/2 x 1/6 = 1/12.
E como seria na regra do OU? Qual é a probabilidade de coroa na moeda OU 2 no dado?
hoje é meu primeiro dia neste blog, achei por acaso, e ja resolvi maior parte de duvidas de estatistica que tinha, adorei o blog e vou seguir.
De:Moçambique
(Qual é a probabilidade de coroa na moeda OU 6 no dado?)
todas as repostas que foram dadas a essa pergunta estão erradas!
porque:
igual o exemplo do rei ou copas...
deve subtrair a probabilidade de repetições...
logo 1/6 + 1/2 esta ERRADO, por favor professores da vida ensinem isso também...
O CERTO SERIA >>>>> 1/6 + 1/2 - 1/12
O 1/12 é a Probabilidade de repetições... sair cara e tambem sair 6
No fim se ainda existe alguém que ache que estou errado...
faca a prova real verificando todos os anagramas e também reflitam sobre a necessidade de uma subtração em alguns casos pois se assim não fosse... 1/2 + 1/2 = 100%
b) Qual é a probabilidade de, ao se tomar um número ao acaso, o número ser um ímpar ou múltiplo de 3?
a resposta correta não é 3/5.
a resposta é 4/6
3/5 = 0.6
4/6 = 0.666666667
explicação:
# dados
Probabilidade de se um número par >>> 1/2
P/ de múltiplo de 3 >>> 1/3
P/ de ser par E múltiplo de 3 >>> 1/3 * 1/2 = 1/6
Então de acordo com a própria explicação a respeito da exceção da regra do OU... deve subtrair o resultado as repetições... ou seja 1/6
Então no final fica:
1/2 + 1/3 - 1/6
=
3/6 + 2/6 - 1/6
=
4/6
Obrigada, o cumprimento ajuda.
Obrigada, Jônatas, pela correção de minha resposta à pergunta:
"Vamos refazer a pergunta, para facilitar a discussão. Jogam-se um dado e uma moeda. O jogador ganha se sair “cara” na moeda ou “2” no dado. Qual é a probabilidade de o jogador ganhar em um só arremesso?"Refiz no texto, por facilidade do uso de sinais gráficos.
Quanto à questão b que segue, ainda acho que estou certa, mas não está clara a pergunta:
É dado o conjunto de dados: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10.
a) Qual é a probabilidade de, ao se tomar um número ao acaso, o número ser um ímpar menor do que 4 ou um ímpar maior do que 8?
b) Qual é a probabilidade de, ao se tomar um número ao acaso, o número ser um ímpar ou múltiplo de 3? Refiz esta pergunta e coloquei seu problema no texto. OBRIGADA.
Minhas desculpas ao ProJovem Núcleo Magalhães Drummond que em 22/8/18 me dirigiu uma pergunta que respondi errado. Só agora, 10/4/19 fui corrigida, por Jônatas Pereira de Campos. Coloquei a resposta dele no texto, pela facilidade de sinais gráficos. E quero deixar claro: toda correção é bem vinda. Nosso ofício é ensinar, ensinar certo.
OK👍
Ficou muito bom agora e fácil de entender!
Ótimo trabalho Sonia Vieira!
acredito que nesse caso faz o mmc
Seu blog é excelente. Parabéns.
Post a Comment