Para bem
entender o teorema da multiplicação de probabilidades, ajuda pensar o teorema
dividido em duas regras: a regra nº 1, para a multiplicação de eventos
independentes e a regra nº 2, para a multiplicação de eventos
dependentes. Veja primeiro “regra número 1”.
Eventos independentes

Na vida real encontramos muitos exemplos de eventos independentes. Por exemplo, “chover hoje” e “ser feriado amanhã” são eventos independentes porque o fato de “chover hoje” não muda a possibilidade de “ser feriado amanhã”, nem o fato de “ser feriado amanhã” muda a possibilidade de “chover hoje”. Na área de saúde, existem vários exemplos de eventos independentes: o fato de uma pessoa ser míope não afeta a probabilidade de ter cárie dentária; a profissão não afeta a probabilidade de uma pessoa ter cálculos renais; o estado civil do cidadão não modifica a probabilidade de ser calvo.
Regra 1 da multiplicação
(para eventos independentes)
Se A e B são eventos independentes, a probabilidade de ocorrer A e B é dada pela probabilidade de ocorrer A, multiplicada pela probabilidade de ocorrer B. Escreve-se:
Exemplo
Se
a ocorrência do evento A modifica a probabilidade de ocorrência do evento B,
dizemos que esses dois eventos, A e B, são dependentes.
Exemplo
Há
seis meias em uma gaveta: três vermelhas e três azuis. Você quer um par de
meias vermelhas. Sem olhar, você retira uma meia da gaveta. É vermelha. Sem
recolocar essa meia de volta na gaveta, você retira uma segunda meia. Nesta
segunda retirada, a probabilidade de a segunda meia ser vermelha é menor. Por
quê?
Na 1ª retirada você tinha três meias
vermelhas em seis, ou seja, metade das meias era vermelha.
Na 2ª retirada você tinha duas meias vermelhas em cinco,
ou seja, menos da metade das meias eram vermelhas. A
probabilidade de sair meia vermelha na primeira retirada modifica a
probabilidade de sair meia vermelha na segunda retirada. Dizemos então que
esses eventos são dependentes.
Probabilidade condicional
Probabilidade
condicional de B dado A é
a probabilidade de ocorrer o evento B sob a condição de
o evento A ter ocorrido. Indica-se por P(B|A),
que se lê “probabilidade de B dado A”.
Exemplo
Há
seis meias na gaveta: três vermelhas e três azuis. Você quer um par de meias
vermelhas. Sem olhar, retira uma meia da gaveta e, sem recolocar essa meia na
gaveta, retira outra. Qual é a probabilidade de ambas serem vermelhas?
Você tem aí uma probabilidade condicional: probabilidade de sair uma segunda meia vermelha dado que a primeira era vermelha. Em outras palavras, foi calculada a probabilidade de sair uma segunda meia vermelha sob a condição de a primeira meia retirada ser vermelha.
Toda vez que calcularmos a probabilidade condicional de B dado A,
devemos lembrar que o espaço amostral fica reduzido – a
condição de o evento A ter ocorrido diminui o espaço amostral para a ocorrência
do evento B.
Exemplo
Para responder a primeira questão, você tem seis eventos no
espaço amostral e apenas um deles é de interesse. Para
responder a segunda questão, você tem três eventos no espaço
amostral e, também, apenas um deles é de interesse. Então
Regra
2 da multiplicação
(para eventos dependentes)
Se A e B são eventos
dependentes, a probabilidade de ocorrer A e B é
dada pela probabilidade de ocorrer A multiplicada pela
probabilidade de ocorrer B dado que A ocorreu
(esta probabilidade é condicional). Escreve-se:
Exemplo
Cinco
bolas que se distinguem apenas pela cor são colocadas dentro de um chapéu e
perfeitamente misturadas. Três dessas bolas são azuis e duas são vermelhas.
Retiram-se duas bolas ao acaso do chapéu, sem olhar, uma em seguida da outra e
sem que a primeira tenha sido recolocada. Qual é a probabilidade de que as duas
sejam vermelhas?
O
chapéu contém cinco bolas: duas são vermelhas. Então a probabilidade de a
primeira bola retirada ser vermelha é
Como
a bola retirada não foi recolocada, restam quatro bolas no chapéu. Se a
primeira bola retirada era vermelha, das quatro bolas que ficaram no
chapéu apenas uma é vermelha. A probabilidade (condicional) de a segunda
bola retirada ser vermelha é:
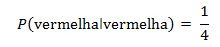
A
probabilidade de as duas bolas retiradas serem vermelhas é dada pelo produto:
Dois eventos são independentes se a probabilidade de que ocorram juntos é igual ao produto das probabilidades de que ocorram em separado, uma vez que a ocorrência de um deles em nada ajuda a ocorrência do outro.
Exemplo
A
questão da independência é bem ilustrada pelo jogo
de uma moeda duas vezes: o resultado do primeiro lançamento não influi no
resultado do segundo lançamento. Os dois eventos são independentes.
Veja probabilidade em:





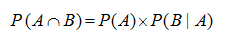



6 comments:
Estou estudando a alguns dias para.concurso com um professor excelente mas a única.dúvida ainda era multiplicação de probabilidade e você esclareceu de uma.forma muito didática! Parabéns! Deus te abençoe!
Eu jogo dados e nem por isso eu calculo a probabilidade deles. Eu apenas jogo.
Excelente post sobre o assunto. Didático e direto ao assunto. Obrigada por disponibilizá-lo.
Muito obrigado ^^
excelente posto!!!
parabéns
Muito bem explicado !!
Post a Comment