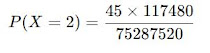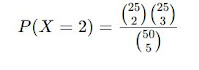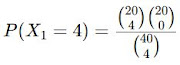Distribuição hipergeométrica: exercícios com solução

                                                               ⚠️   Exercícios   

1.     🤯Dos 25 itens de um lote finalizado em uma linha de produção, 2 eram não conformes. Foram retirados ao acaso 4 itens para inspeção. a) Calcule a probabilidade de os 4 itens amostrados serem conformes. b) A amostra pode ter 3 itens não conformes?  Imagine que uma fábrica produz parafusos, e um lote de 100 parafusos contém 10 defeituosos. Você seleciona uma amostra aleatória de 5 parafusos sem reposição. Qual é a probabilidade de encontrar exatamente 2 parafusos defeituosos na amostra? 

      Dados:                  

          N =100 (total de parafusos)

          N₁ =10 (parafusos defeituosos)

          n = 5 (parafusos na amostra)

          x₁ =2 (exatamente 2 defeituosos na amostra)

A probabilidade é:

                                      

   Cálculo dos coeficientes binomiais:

      Agora, calculamos a probabilidade:

   🔚A probabilidade pedida aproximadamente 0,0702 ou  7,02%.

2. 🤯 Um hospital está testando um novo tratamento para uma doença rara. Em um grupo de 50 pacientes, 25 receberam o tratamento experimental e 25 receberam um tratamento padrão. Para um estudo mais detalhado, os médicos selecionam aleatoriamente 5 pacientes sem reposição para exames laboratoriais mais aprofundados. Qual é a probabilidade de que exatamente 2 dos 5 pacientes selecionados tenham recebido o tratamento experimental?

 Dados:

                  N = 50 (total de pacientes)

                  N₁ = 25 (pacientes com tratamento experimental)

                  n = 5 (pacientes selecionados)

                  x₁ = 2 (exatamente 2 receberam tratamento experimental)

A fórmula é a mesma:

Cálculo dos coeficientes binomiais

 Agora, calculamos a probabilidade:

🔚A probabilidade de selecionar 2 pacientes que receberam o tratamento experimental na amostra de 5 é 0,3257 (ou aproximadamente 32,57%. 

3.  🤯 Entre os dez pares de meias de uma pessoa, quatro pares precisam de conserto. Se ela escolher aleatoriamente três desses pares para levar em uma viagem, qual é a probabilidade de que um par precise de conserto?

    🔚A probabilidade de selecionar um par que precisa de conserto é 0,5 ou 50%.

      4. 🤯Entre os 16 caminhões de entrega de uma loja de departamentos, cinco têm freios

       desgastados. Se três dos caminhões forem aleatoriamente marcados para uma revisão,

       qual é a probabilidade de que dois tenham freios desgastados?

                  N = 16 (total de caminhões)

                  N₁ = 5 (freios desgastados)

                  n = 5 (caminhões marcados para revisão)

                  x₁ = 2 ( 2 com freios desgastados)

                                          

       🔚A probabilidade de selecionar 2 caminhões com freios desgastados é 19,64%%.

           5 .🤯 Numa prisão federal para mulheres, 31 das 102 reclusas têm opiniões políticas

           radicais. Se cinco delas forem escolhidas aleatoriamente para comparecer perante

           um comitê legislativo, encontre a probabilidade de que apenas uma delas tenha visões                           políticas radicais.

                  Dados

                  N = 102 (total de reclusas)

                  N₁ = 5 (opiniões políticas radicais)

                  n = 5 (cinco escolhidas)

                  x₁ = 1 ( 1 opiniões políticas radicais)

    🔚A probabilidade de  1 reclusa com opiniões políticas radicais estar na amostra é

                   0,3616 ou 36,16%.

6. 🤯Há 5 pessoas em uma sala: 3 foram vacinadas contra a gripe e 2 não foram vacinadas. Toma-se uma amostra de 3 pessoas. a) Construa uma tabela para apresentar os dados. b) Qual é a probabilidade de as 3  terem sido vacinadas?

                  N = 5 (total de pessoas)

                  N₁ = 3 (vacinadas)

                  N₂ = 2 (não vacinadas)

                  n = 3 (cinco escolhidas)

                  x₁ = 3 (vacinadas)

                          

  🔚A probabilidade de  as três pessoas vacinadas  estarem na amostra é 0,10 ou 10,0%. 

7. 🤯Um baralho tem 52 cartas, das quais 26 são vermelhas e 26 são pretas. 

Você tira uma carta ao acaso. Qual é a probabilidade de você ter tirado uma carta vermelha? 

São 52 possibilidades, das quais 26 são favoráveis. Então a probabilidade de sair uma carta “vermelha” é 0,5 ou 50%. Simples, não é? Mas vamos complicar. Vamos ver o problema como uma hipergeométrica. 

Temos um baralho de 52 cartas (N = 52). Metade é de cartas vermelhas (N1= 26) e metade é de cartas pretas (N2 =26). Tira-se uma carta (n = 1) ao acaso. Qual é a probabilidade de essa carta ser vermelha  (x1)? Construa uma tabela para apresentar esses dados e calcule a probabilidade pedida usando a hipergeométrica.

                                                                               

       🔚A probabilidade de  a carta ser vermelha é 0,50 ou 50,0%. 

Distribuição hipergeométrica: conceitos, cálculos e gráficos

                                                           

                                                                Definição 

Distribuição hipergeométrica é uma distribuição discreta que descreve o número de sucessos (X₁) em uma amostra de tamanho fixo (n), retirada sem reposição de uma população finita de tamanho conhecido (N). Cada item na amostra tem dois resultados possíveis: sucesso ou fracasso. São conhecidos os números de sucessos (N₁) e de fracassos (N₂) na população.

A distribuição hipergeométrica é definida pelos seguintes parâmetros:

·      N: Tamanho total da população

·     N₁: Número de sucessos na população

·     n: Tamanho da amostra retirada

Um gráfico de barras mostra como a probabilidade varia para diferentes valores de X₁​.

Interpretação e Aplicações 

Este exemplo ilustra como a distribuição hipergeométrica é utilizada para analisar situações em que amostras são retiradas sem reposição de uma população finita. Portanto, essa distribuição é apropriada para calcular a probabilidade de obter determinado número de sucessos em uma amostra, sabendo a quantidade total de sucessos e fracassos na população.

                                                  Observações Importantes 

1. A distribuição hipergeométrica é utilizada quando o tamanho da população total é conhecido e deseja-se calcular a probabilidade de retirar um número específico de itens com uma determinada característica. Por exemplo, você quer saber a probabilidade de retirar sequencialmente, quatro cartas de ouros em uma sequência de 4 retiradas. 

2.  A probabilidade de selecionar determinado item muda a cada retirada, pois não há reposição. No exemplo das cartas de baralho, a probabilidade de sair uma carta de ouros na primeira retirada é 13/52​. Se uma carta de ouros foi retirada, a probabilidade de sair uma carta de ouros na segunda retirada é 12/51​.

   Função de probabilidade da distribuição hipergeométrica

A função de probabilidade da distribuição hipergeométrica é dada por:    

                                       
                                                          Exemplo 1

Imagine uma caixa com 20 bolas vermelhas e 20 bolas azuis. Quatro bolas são retiradas da caixa ao acaso, sem reposição. Seja X_1​ o número de bolas vermelhas retiradas. Então, X₁ ​ é uma variável aleatória que pode assumir os valores: 0, 1, 2, 3 ou 4. Vamos analisar a distribuição de X₁​, isto é, calcular a probabilidade de X₁​ assumir cada um dos valores possíveis na amostra.

                                         Definições e Parâmetros

·      N = 40:   Total de bolas na caixa

·      N₁ = 20: Número de bolas vermelhas na caixa (sucessos)

·     N₂ = 20: Número de bolas azuis na caixa (fracassos)

·      n = 4:     Tamanho da amostra retirada

·      X₁ = 0,1,2,3,4: Possíveis valores para a variável aleatória

                                Cálculo das probabilidades

Para calcular as probabilidades associadas a cada valor de X₁​, utilizamos a distribuição hipergeométrica:

                                                     

Vamos organizar os resultados em uma tabela, mostrando os valores de X₁​ e suas respectivas probabilidades. Em seguida, apresentaremos esses resultados em um gráfico de barras para visualizar a distribuição.

                                                                    Tabela 1

                                        Valores de X₁​ e suas respectivas probabilidades

 

É trabalhoso calcular todas essas probabilidades manualmente. No entanto, é possível utilizar uma calculadora online. Uma opção é:

                                   Hypergeometric Distribution Probability Calculator

                                                                  Gráfico 1

                                  Valores de X₁​ e suas respectivas probabilidades

                                                            Exemplo 2

Imagine agora uma caixa com 20 bolas vermelhas e 4 bolas azuis. Quatro bolas são retiradas ao acaso, sem reposição. Seja X₁​ o número de bolas vermelhas retiradas.

                                                      Definições e Parâmetros

·      N = 24:  Total de bolas na caixa

·      N₁ = 20: Número de bolas vermelhas (sucessos)

·      N₂ = 4:  Número de bolas azuis (fracassos)

·       n = 4:   Tamanho da amostra retirada

·      X₁ = 0,1,2,3,4 

                                                                Tabela 2

                              Valores de X₁​ e suas respectivas probabilidades

                                                  
                                               

                                                         Gráfico 2

                                         Valores de X₁​ e suas respectivas probabilidades

                      

O gráfico mostra as probabilidades associadas aos diferentes valores de X₁​.

                                  Comparação entre as Distribuições

           Gráfico 1: A distribuição é simétrica, pois o número de sucessos e fracassos na população é igual.

     Gráfico 2: A distribuição é assimétrica, pois há um número significativamente maior de sucessos (vermelhas) do que fracassos (azuis).

Média e Variância na Distribuição Hipergeométrica

Para a distribuição hipergeométrica, a média e a variância são dadas por:   

                                         

       

          O último multiplicador é o fator de correção para amostra finita

  Definições e Parâmetros

                             

·      N:    Tamanho total da população

·     N₁​: Número de sucessos na população

·      n:    Tamanho da amostra retirada

       

                                                        Exemplo 3

Considere uma população com N = 50 unidades, das quais N₁ = 20 possuem a característica de interesse. Retiramos uma amostra de n = 10 unidades e analisamos as probabilidades para diferentes quantidades de unidades de interesse na amostra. Calcule as probabilidades e faça um gráfico. Depois, calcule a média e a variância da distribuição.

 Dica: use algum recurso computacional para fazer cálculos e gráfico. 

                                                                  Gráfico 3

  Cálculo da Média

                                                           Cálculo da Variância

                                                             Resultados

A média e a variância da distribuição hipergeométrica para N = 50, N₁ = 20 e n = 10 são:

 Média (μ) = 4

 Variância (σ²) ≈ 1,958

Considerações Finais

A distribuição hipergeométrica é particularmente útil em situações onde não há reposição na retirada de amostras de uma população finita. Os exemplos apresentados mostram como utilizar essa distribuição para calcular probabilidades e como interpretar a simetria ou assimetria dos gráficos, dependendo da relação entre sucessos e fracassos na população.