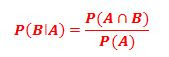Teorema de Bayes e teste diagnóstico na Genética

Antes de ver o exemplo, convém ler, neste mesmo blog, as postagens:
            Teorema de Bayes 
            Testes diagnósticos: sensibilidade e especificidade.

Considere a porfiria, uma doença autossômica dominante. Toda pessoa afetada tem um genitor afetado e tem 50% de chance de transmitir o gene (e consequentemente a doença) para os filhos. Veja o heredograma, em que verde indica pessoa sem a doença e vermelho indica pessoa afetada.

 

Existe um teste para o diagnóstico precoce da doença, que tem sensibilidade  0,82 e especificidade é 0,963.

Situação 1: Uma pessoa teve resultado positivo no teste para a porfiria. Qual é a probabilidade de essa pessoa ter a doença?

Sem qualquer informação adicional, a resposta é óbvia: se a sensibilidade do teste (probabilidade de verdadeiros positivos no total de doentes) é 0,82, a probabilidade de essa pessoa ter porfiria é 0,82 ou 82%.

Situação 2: A porfiria é uma doença rara, que ocorre na população com probabilidade 0,01%. Se uma pessoa tomada ao acaso da população obtiver resultado positivo no teste para a doença, qual é a probabilidade de ela ter a doença?

Como a sensibilidade do teste é 0,82 e a especificidade é 0,963, a probabilidade de a pessoa, que teve resultado positivo no teste diagnóstico ter a doença deve ser obtida pelo teorema de Bayes. Veja o diagrama de árvore. Observando o diagrama, fica mais fácil calcular a probabilidade de a pessoa ter porfiria, dado que o teste positivou.

Situação 3: A porfiria é uma doença autossômica dominante. É dada a informação adicional de que uma pessoa que fez o teste tem um irmão germano com porfiria. Se o resultado no teste foi positivo, qual é a probabilidade de essa pessoa ter a doença?

A probabilidade de um paciente que tem irmão com a doença ter porfiria se tiver resultado positivo no teste é obtida pelo teorema de Bayes. Observe o diagrama de árvore e calcule a probabilidade pedida.

Situação 4: Uma pessoa  não conhece seu histórico genético familiar (digamos foi adotada bebê), mas um médico experiente tem o palpite de que a  probabilidade de essa pessoa ter a porfíria é 30%. Se a pessoa positivar no teste, qual é a probabilidade de essa pessoa ter porfiria? 

A probabilidade é obtida aplicando o teorema de Bayes. Veja o diagrama de árvore e o cálculo abaixo.

Pense nisto: para a mesma pergunta – qual é a probabilidade de a pessoa ter a doença? – foram obtidas respostas  diferentes. Por quê?

O teorema de Bayes permite rever um valor calculado de probabilidade com base em informação anterior. Qual das respostas é a correta? Depende da situação:

v  Na 1ª situação, a probabilidade de a pessoa ter a doença foi obtida apenas pela sensibilidade do teste.

v  Na 2ª situação, a probabilidade foi obtida considerando a baixa prevalência na população, conhecida por grandes levantamentos (surveys) feitos anteriormente.

v  Na 3ª situação, a probabilidade a priori foi obtida considerando, em seu cálculo, conhecimento de genética e a história familiar do paciente.

v  Na 4ª situação, a probabilidade foi obtida levando em conta o palpite (educated guess) do médico, ou seja, a partir de intuição clínica.

                                   IMPORTANTE

O teorema de Bayes permite incorporar conhecimentos anteriores aos fatos observados: usamos um valor de probabilidade a priori (obtida antes de saber o resultado do teste) para mais bem estimar uma probabilidade a posteriori, obtida dos dados observados. 

       Este exemplo é de 
             Motulsky, H. Intuitive Biostatistics.Oxford universityPress. 

                 1995. P133-6.

Probabilidades de Trás pra Frente: A Lógica do Teorema de Bayes

Antes de apresentar o Teorema de Bayes, convém relembrar a definição de probabilidade condicional, para destacar a diferença entre este conceito e o próprio teorema.

❗  Definição

A probabilidade condicional de um evento B dado que ocorreu o evento A é a chance de ocorrer B sob a condição de que A tenha ocorrido. Representa-se por P(B∣A), que se lê: “probabilidade de B dado A”.    

                          

É importante observar que:

🔸   A e B são eventos dependentes.

🔸  O evento A ocorre antes do evento B.

                                      🛑   Exemplo

Uma urna contém cinco bolas que se diferenciam apenas pela cor: duas vermelhas e três azuis. Retiram-se duas bolas sem reposição, uma após a outra.

Pergunta: Qual a probabilidade de a segunda bola ser vermelha, sabendo que a primeira era azul?

Um diagrama de árvore ajuda a visualizar os possíveis desfechos nessa situação. Todas as probabilidades condicionais são indicadas, e a resposta à pergunta está destacada em amarelo.

          

A resposta é dada pela regra da multiplicação de probabilidades para eventos dependentes:

❗   TEOREMA DE BAYES

⚠️P(B∣A) e P(A∣B) podem parecer símbolos semelhantes, mas representam coisas diferentes. Veja dois exemplos:

1.     Seja A: “ter treinamento técnico”. Seja B: “executar um bom serviço”.

🔸 P(B∣A): probabilidade de executar um bom serviço dado que tem treinamento técnico.

🔸 P(A∣B): probabilidade de ter treinamento técnico dado que executou um bom serviço.

2.     Seja A: “ter sido bom aluno no colegial”. Seja B: “ter sido aprovado no vestibular”.

🔸 P(B∣A): probabilidade de aprovação no vestibular dado que foi bom aluno.

🔸 P(A∣B): probabilidade de ter sido bom aluno dado que foi aprovado no vestibular.

Esses pares de probabilidades aparecem frequentemente em problemas reais. Vamos buscar agora uma fórmula para calcular P(A∣B).

                  

Igualando as expressões:

$$$$

Isolando P(A∣B):

         

🛑 Exemplo – Aplicando o Teorema de Bayes

Vamos voltar ao exemplo das bolas da urna, agora com uma pergunta diferente:

Pergunta: Qual é a probabilidade de a primeira bola retirada ter sido uma bola azul, sabendo que a segunda era vermelha?

Pelo diagrama de árvore, vemos que a segunda bola ser vermelha pode ocorrer de duas maneiras:

                                     ·  Azul e vermelha (A-Z)

                                     ·  Vermelha e vermelha (V-V)

O evento de interesse é: primeira azul dado segunda vermelha, isto é:

$$\mathrm{<span\; class="vlist-s"\; style="text-align:\; justify;"><span\; face="Verdana,\; sans-serif">Aplicamos\; o\; teorema\; de\; Bayes.\; Mas\; vamos\; formalizar.</span></span>}$$

Teorema de Bayes: Sejam A e B dois eventos dependentes que ocorrem em sequência, A antes de B. A probabilidade de ocorrer A sob a condição de B ter ocorrido é dada por: 

Observe o esquema abaixo: está marcado o evento de interesse, que é a probabilidade de ocorrer A dado que B tenha ocorrido. Mas B pode ocorrer de duas maneiras: depois de A e depois de A -traço.

$$\mathrm{<span\; class="vlist-s"\; style="text-align:\; justify;">\; </span><span\; class="vlist-s"><span\; style="text-align:\; center;"><span\; style="font-size:\; medium;"><b><br></b></span></span></span><span\; class="vlist-s"><span\; style="text-align:\; center;"><span\; style="font-size:\; medium;"><b> \; \; \; \; \; \; \; \; \; \; \; </b></span></span></span>}$$🔔 Interpretação

O Teorema de Bayes inverte a ordem da informação:

$$$$

      ·  A probabilidade condicional trata de P(B∣A): probabilidade de ocorrer B dado que ocorreu A.

$\mathrm{}$

     ·  O Teorema de Bayes trata de  P(A∣B): probabilidade de ocorrer A dado que ocorreu B, ou seja, o reverso da probabilidade condicional.

🛑 Exemplo – Teste do bafômetro

Em uma cidade, o teste do bafômetro é obrigatório.

                  ·      25% dos motoristas bebem antes de dirigir.

                  ·      Dos que bebem, 99% testam positivo.

                  ·      Dos que não bebem, 17% também testam positivo.

Pergunta: Se um motorista testou positivo, qual a chance de ele ter realmente ingerido bebida alcoólica?

Use os eventos: B: bebe; NB: não bebe ;+: teste positivo

$<o:p></o:p>$

$<math\; display="block"\; xmlns="http://www.w3.org/1998/Math/MathML"><semantics><mrow><mi></mi></mrow></semantics></math>$

A probabilidade pedida é:

  🛑 Exemplo – Corrida de cavalos

Dois cavalos correm: Branco e Negro.

·  Em 12 corridas anteriores, Branco venceu 5 vezes e Negro 7.

·  Em 3 das 5 vitórias de Branco, chovia.

·  Em 1 das 7 vitórias do Negro, também chovia.

Está chovendo agora. Qual a probabilidade de Branco vencer?

O que queremos é:

Use os dados no diagrama de árvore para encontrar a probabilidade: $\frac{\mathrm{<span\; style="font-family:\; verdana;"><span\; style="font-size:\; small;">3/4.</span></span>}}{}$

$\frac{\mathrm{<span\; style="font-family:\; verdana;"><span\; style="font-size:\; small;"><br></span></span><span\; style="font-family:\; verdana;"><span\; style="font-size:\; small;"> \; \; \; \; \; \; \; \; \; \; \; \; **************************</span></span>}}{}$

Nota: 1. Thomas Bayes (1702-1761) foi um pastor presbiteriano e matemático inglês, conhecido por ter formulado o caso especial do teorema de Bayes.