Para quem este post é útil?
Se você usa matrizes apenas em cálculos
aplicados — por exemplo, em regressão linear usando software — não precisa
decorar essas propriedades. Mas se está em uma pós-graduação, estuda teoria da
álgebra linear ou faz cálculos de determinantes à mão, essas propriedades são
fundamentais.
1ª Propriedade – Troca de linhas (ou colunas)
Trocar duas linhas (ou colunas) inverte o
sinal do determinante.
Exemplo:
Trocando as linhas:
2ª Propriedade – Multiplicação de linha (ou coluna) por escalar
Se multiplicar uma linha por k, o
determinante é multiplicado por k.
Exemplo:
Multiplicando a segunda linha por 5:
3ª Propriedade – Linha ou coluna nula
Se uma linha ou coluna for composta apenas
de zeros, o determinante é zero.
Exemplo:
4ª Propriedade – Linhas (ou colunas) iguais
Se duas linhas ou colunas são iguais, o
determinante é zero.
Exemplo:
5ª Propriedade – Linhas (ou colunas) proporcionais
Se uma linha é múltipla exata de outra, o
determinante é zero.
Exemplo:
6ª Propriedade – Matriz triangular
Se a matriz é triangular (superior ou
inferior), o determinante é o produto dos elementos da diagonal principal.
Exemplo:
7ª Propriedade – Transposta da matriz
O determinante não muda quando se toma a
transposta da matriz.
Exemplo:
Conclusão
Essas propriedades não são só teóricas. Elas ajudam a:
🔹Detectar determinantes nulos
🔹Simplificar matrizes antes de expandir
🔹Verificar resultados de forma eficiente
📘 No próximo post: Operações com
matrizes — como somar, subtrair e multiplicar.



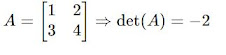

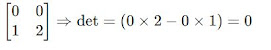




No comments:
Post a Comment