A regra de Sarrus é um método para calcular o determinante de uma matriz 3 x 3. Na verdade, é um atalho que permite achar o valor do
determinante de uma matriz 3x3 de maneira segura – e muito mais rápida do que
aplicando a fórmula geral para o cálculo do determinante de uma matriz quadrada
de ordem n.
Métodos que simplificam cálculos são pouco
valorizados hoje em dia, porque o calculista sempre argumenta que usa um
software estatístico. Mas se você não quiser apenas entregar um “resultado” ao
chefe, mas quiser conhecer os percalços do caminho, veja o procedimento para se chegar
à regra de Sarrus.
Seja a matriz 3 x3 D, é trabalhoso achar o determinante:
Para entender a regra de Sarrus, vamos reescrever o determinante da matriz D colocando, em primeiro lugar, os três termos com sinais positivos e, depois, os três termos com sinais negativos:
Observe que todas
as parcelas são formadas pelo produto de três elementos. Veja como construir as
parcelas com sinal positivo:
🔹 a primeira
parcela com sinal positivo do determinante é dada pelo produto dos elementos da
diagonal principal, indicada pela flecha na Figura 1.
🔹 a segunda parcela com
sinal positivo do determinante é dada pelo produto dos elementos marcados em
vermelho na Figura 1.
🔹 a terceira parcela com sinal positivo do determinante é dada pelo produto dos elementos marcados azul na Figura 1.
Veja como
construir as parcelas com sinal negativo:
🔹 a primeira parcela com sinal negativo do determinante é dada pelo produto dos elementos da diagonal secundária, indicada pela flecha na Figura 2.
🔹 a segunda parcela
com sinal negativo do determinante é dada pelo produto dos elementos marcados
em vermelho na Figura 2.
🔹 a terceira
parcela com sinal negativo do determinante é dada pelo produto dos
elementos marcados em azul na Figura 2.
A soma das seis parcelas
– três com sinal positivo, três com sinal negativo – dá o determinante. Esta
regra prática denomina-se Regra de Sarrus.
Exemplo
Calcule o determinante da matriz:
Aplicando a Regra de Sarrus:


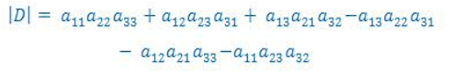



No comments:
Post a Comment