1º Exemplo: Na população branca do Brasil,
85% têm Rh+. Três pessoas são amostradas ao acaso dessa população.
Construa a distribuição binomial e faça um gráfico.
n é o número de pessoas: n = 3
X é o número de pessoas com Rh+ na amostra
p é a probabilidade de Rh+: p = 0,85
q é a
probabilidade de Rh-: q = 0,15.
Cálculos intermediários para obter a distribuição binomial
Para construir a tabela de distribuição binomial, some probabilidades de eventos que levam ao mesmo valor de X. A distribuição é dada na tabela a seguir.
Distribuição de probabilidades
do número de pessoas com Rh+, numa amostra de três pessoas
2º Exemplo: A probabilidade de um menino ser daltônico é 8%. Qual é a probabilidade de serem daltônicos todos os quatro meninos que se apresentaram, em determinado dia, para um exame oftalmológico?
No problema, p =
0,08. Então q = 1 – 0,08 = 0,92. O número de meninos é n =
4. Para obter a probabilidade de x assumir valor 4, aplica-se
a fórmula:
3º Exemplo: O resultado do cruzamento de ervilhas amarelas homozigotas (AA) com ervilhas verdes homozigotas (aa) são ervilhas amarelas heterozigotas (Aa). Se estas ervilhas forem cruzadas entre si, ocorrem ervilhas amarelas e verdes na proporção de 3 para 1. Portanto, a probabilidade de, num cruzamento desse tipo, ocorrer ervilha amarela é p = 3/4 e a probabilidade de ocorrer ervilha verde é q = 1/4. Logo, o número de ervilhas amarelas em um conjunto de n ervilhas é uma variável aleatória com distribuição binomial de parâmetros n e p = 3/4. Foram pegas, ao acaso, 4 ervilhas resultantes do cruzamento de ervilhas amarelas heterozigotas. Qual é a probabilidade de 2 dessas 4 ervilhas serem de cor amarela?
A probabilidade de 2 das 4 ervilhas serem amarelas é dada por:
4º Exemplo: A probabilidade de um casal
heterozigoto para o gene da fenilcetonúria (Aa × Aa) ter um filho
afetado (aa) é 1/4. Se o casal tiver três filhos, qual é a probabilidade de ter
um filho com a doença?
5º Exemplo: Suponha que, em uma população
parental de moscas das frutas, a frequência de alelos para o fracasso (F)
de um inseticida usado no combate de moscas seja ½ e a frequência de alelos
para sucesso (S) seja ½.
· Frequência
de alelos para fracasso (F) = ½.
· Frequência
de alelos para sucesso (S) = ½.
A frequência de gametas F e S na
população é a mesma, ou seja:
· Frequência
de gametas para fracasso (F) = ½.
· Frequência
de gametas para sucesso (S) = ½.
No caso de organismos diploides,
os gametas distribuem-se de acordo com uma distribuição binomial, uma vez que
são possíveis apenas dois resultados em cada tentativa, ou seja, ou S ou F.
Lembre-se de que
.JPG)
Vamos supor que apenas três zigotos sobreviveram quando o inseticida foi aplicado.
1ª questão: Qual é a probabilidade de
que os três sejam homozigotos FF?
n = 2N gametas na
amostra = 6
x =
número de gametas F na amostra = 6
2º questão: Qual é a probabilidade de
que cada um dos três zigotos tenham genótipos diferentes? Em outras palavras,
qual é a probabilidade de obter FF, FS, SS?
Esta seria a probabilidade de
que três gametas tenham o alelo F e três tenham o alelo S. Então:
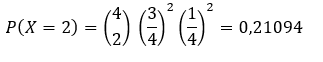
No comments:
Post a Comment