A Função Logística e sua Aplicação na Modelagem de Crescimento

As Funções assintótico-sigmoides

As funções assintótico-sigmoides desempenham um papel importante em estudos de crescimento, sejam eles de natureza biológica, econômica ou demográfica, para os quais os modelos lineares são, muitas vezes, inadequados.

O ajuste dessas funções aos dados de crescimento baseia-se na observação de que, quando representados graficamente, esses dados formam uma curva assintótico-sigmoide, ou seja, apresentam tendência à estabilização (possuem assíntota e têm forma de S).

Diversas funções matemáticas possuem essa característica assintótico-sigmoide. No entanto, no contexto do crescimento, apenas em alguns casos há informações bem definidas sobre a relação entre as variáveis, caracterizando a função, ou existe uma equação diferencial que a função deve, obrigatoriamente, satisfazer.

O ajuste dessas funções pode ser desafiador, mas, atualmente, softwares amplamente disponíveis facilitam essa tarefa. No entanto, o problema fundamental persiste: como escolher a função matemática mais adequada para descrever determinado conjunto de dados de crescimento.

                                   A Função Logística

A função logística é uma das principais funções assintótico-sigmoides utilizadas para modelar o crescimento. Ela é definida por três parâmetros, a, b, e c:

                            

Essa função é monotonicamente crescente e situa-se entre duas assíntotas, Z=0 e Z=a. O parâmetro a, que representa a distância entre essas duas assíntotas, é conhecido como "nível de saturação". O parâmetro c está relacionado à taxa de crescimento de Z, uma vez que

                                       

O parâmetro b é chamado de "parâmetro de posição", pois altera a posição horizontal da curva quando os outros dois parâmetros são mantidos constantes.

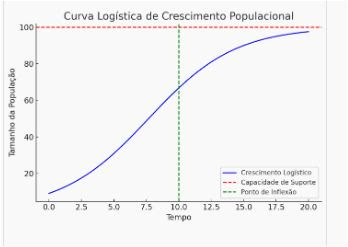
A função logística (1) possui um ponto de inflexão para a abscissa t=−b/c, no qual Z assume o valor a/2. Ainda, a curva logística é radialmente simétrica em torno desse ponto de inflexão.

O uso da função logística para descrever o crescimento fundamenta-se na seguinte equação diferencial:

                                                                        A equação (3) mostra que a taxa de crescimento da função logística é proporcional ao valor atual da função (Z) e à diferença entre esse valor e o nível de saturação (a). Reconhece-se, portanto, na logística um “fator de momento” igual a Z e um “fator de contenção” igual a (a - Z). 

          De (3) segue-se que: 

                

Dessa equação, conclui-se que a taxa de crescimento de Z decresce linearmente à medida que Z aumenta.

 Considerações Finais

Devido a suas características peculiares, a função logística é amplamente utilizada para descrever certos tipos de fenômenos de crescimento. No entanto, essas mesmas características podem torná-la inadequada para representar outros  fenômenos. Portanto, a escolha da função matemática apropriada depende da natureza do problema em questão e das propriedades desejadas para a modelagem do crescimento.

                                           v  v  v v