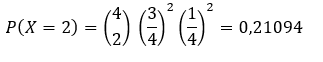Distribuição trinomial : uma extensão da binomial

                         

              🔍   Definição de distribuição trinomial 

Considere $n$ ensaios idênticos e independentes, em que cada ensaio pode resultar em um de três eventos: sucesso, fracasso ou "nenhum deles". Seja $X$ o número de vezes que um ensaio resulta em sucesso, $Y$ o número de vezes que resulta em fracasso e $Z$ o número de vezes que não ocorre nem sucesso nem fracasso.

A probabilidade de ocorrerem $x$ sucessos, $y$ fracassos e $z$ ocorrências do terceiro tipo é dada por:

onde               

              x = 0, 1, …, n

              y = 0, 1, …, n

             x + y ≤ n

         🔍 Quando você tem uma distribuição trinomial?

Você tem uma distribuição trinomial quando tem uma sequência de $n$ eventos (ou $n$ ensaios, ou $n$ tentativas) idênticos e independentes. Em cada evento, são três os resultados possíveis:

·        “sucesso”,

·        “fracasso” e

·        “nenhum deles”.

$$$$

Em todos os eventos, a probabilidade de sucesso (ocorrer o evento de interesse) é $p$, a probabilidade de fracasso é $q$, e a probabilidade de não ocorrer nenhum deles é $\mathrm{1\; -\; (p\; +\; q).<span\; face=""Segoe\; UI\; Emoji",\; sans-serif"\; style="text-indent:\; 0cm;"><br></span>}$

EXEMPLO 1

🔴 Uma urna contém cinco bolas vermelhas, quatro bolas verdes e três bolas azuis, que diferem apenas na cor. Essas bolas estão perfeitamente misturadas. Sem olhar, você retira uma bola, anota a cor e a recoloca na urna, misturando bem. Esse procedimento é repetido 20 vezes.

Qual é a probabilidade de, nessas 20 retiradas, saírem exatamente oito bolas vermelhas e cinco bolas verdes?

                  

Resolução do Exemplo 1

No experimento das bolas na urna, definimos:

• X para o primeiro tipo de resultado (bolas vermelhas),
• Y para o segundo tipo de resultado (bolas verdes),
• Z para o terceiro tipo de resultado (bolas azuis).

Dado que:

n = 20 (tentativas)

x = 8 (bolas vermelhas)

y = 5 (bolas verdes)}

z = 7 (20 - 8 - 5) bolas azuis

 Para calcular a probabilidade pedida, aplicamos a fórmula da distribuição trinomial: 

📢  Resposta: A probabilidade de, nas 20 retiradas, saírem oito bolas vermelhas e cinco verdes é 2,276%.

EXEMPLO 2

🔴 Foram sorteados 20 alunos de uma escola para responder um questionário sobre violência no futebol (2). No sábado anterior, havia tido um jogo importante. A probabilidade de o aluno ter ido ao jogo (evento A) é 0,20, a probabilidade de o aluno ter assistido ao jogo pela TV (evento B) é 0,50 e a probabilidade de o aluno ter ignorado o jogo (evento C) é 0,30. Qual é a probabilidade de, dos 20 alunos sorteados, 4 terem ido assistir ao jogo no campo e 10 alunos terem assistido ao jogo na TV?

No sábado anterior, houve um jogo importante.

As probabilidades são:

·  A probabilidade de o aluno ter ido ao jogo no estádio (A) é 0,20,

·  A probabilidade de o aluno ter assistido ao jogo pela TV (B) é 0,50,

·  A probabilidade de o aluno ter ignorado o jogo (C) é 0,30.

Qual é a probabilidade de, entre os 20 alunos sorteados, exatamente 4 terem ido ao estádio e 10 terem assistido ao jogo na TV?

n = 20

x = 4 (foram ao estádio)

y =10 (assistiram pela TV)

z = 20−4−10=6 (ignoraram o jogo)

Aplicando a fórmula da distribuição trinomial:

                                          P (X = 4, Y = 10, Z = 6) = 0,175%.

📢 Resposta: A probabilidade de, entre os 20 alunos sorteados, exatamente 4 terem ido ao estádio e 10 terem assistido ao jogo na TV ´0,175%

EXEMPLO 3

🔴 Dois enxadristas disputam uma série de 12 partidas. Com base em jogos anteriores, estima-se que:

·  A probabilidade de um deles (chamado de A) vencer é 0,40,

·  A probabilidade do outro jogador (B) vencer é 0,35,

·  A probabilidade de empate é 0,25.

Qual é a probabilidade de A vencer exatamente 7 jogos e B vencer exatamente 2 jogos?

n = 12 (jogos)

x =7 (vitórias de A)

y = 2 (vitórias de B)

z = 12−7−2=3 (empates)

Aplicando a fórmula da distribuição trinomial:

                            P (X = 7, Y = 2, Z = 3) = 0,0248

 

📢  Resposta: A probabilidade de A vencer exatamente 7 jogos e B vencer exatamente 2 jogos é 2,48%

 

EXEMPLO 4

🔴 Em uma pesquisa para a eleição presidencial, 40% dos eleitores disseram preferir o candidato A, 10% disseram preferir o candidato B e os demais afirmaram estar indecisos.

Se você seleciona 10 eleitores ao acaso, qual é a probabilidade de:

·  4 preferirem o candidato A,

·  1 preferir o candidato B,

·  Os demais continuarem indecisos?

n=10 (entrevistados)

x=4 (preferem A)

y=1 (preferem B

z=10−4−1=5 (indecisos)

z = 10 - 4 - 1 = 5

 

                           Aplicando a fórmula da distribuição trinomial:

 

                                          P (X = 4, Y = 1, Z = 5) = 10,08%

📢  Resposta: A probabilidade de, entre 10 eleitores, 4 preferirem A 1 preferir B é 10,08%.

Distribuição binomial na Genética

   

     Lembre-se de que, na distribuição binomial:

Exemplo 1: O resultado do cruzamento de ervilhas amarelas homozigotas (AA) com ervilhas verdes homozigotas (aa) são ervilhas amarelas heterozigotas (Aa).

                                                                  AA x aa

                                                                       Aa

            Se estas ervilhas forem cruzadas entre si, ocorrem ervilhas amarelas e verdes na proporção de 3 para 1. Portanto, a probabilidade de, num cruzamento desse tipo, ocorrer ervilha amarela é p = 3/4 e a probabilidade de ocorrer ervilha verde é q = 1/4.

                                                              Aa x Aa

                                                          AA Aa Aa aa

            Logo, o número de ervilhas amarelas em um conjunto de n ervilhas é uma variável aleatória com distribuição binomial de parâmetros n e p = 3/4. Foram pegas, ao acaso, 4 ervilhas resultantes do cruzamento de ervilhas amarelas heterozigotas.

            Qual é a probabilidade de 2 dessas 4 ervilhas serem de cor amarela? A probabilidade de 2 das 4 ervilhas serem amarelas é dada por:

💡  Resposta: A probabilidade é 21,094%.

Exemplo 2: A probabilidade de um casal heterozigoto para o gene da fenilcetonúria (Aa × Aa) ter um filho afetado (aa) é 1/4. Se o casal tiver três filhos, qual é a probabilidade de ter um filho com a doença?

💡 Resposta: A probabilidade é aproximadamente 42,2%.

 

Exemplo 3: 2º Exemplo: A probabilidade de um menino ser daltônico é 8%. Qual é a probabilidade de serem daltônicos todos os quatro meninos que se apresentaram, em determinado dia, para um exame oftalmológico? No problema, p = 0,08. Então q = 1 – 0,08 = 0,92. O número de meninos é n = 4. Para obter a probabilidade de x assumir valor 4, aplica-se a fórmula: 

💡 Resposta: A probabilidade é aproximadamente 0,0041%.

Exemplo 4: Na população branca do Brasil, 85% têm Rh+. Três pessoas são amostradas ao acaso dessa população. Construa a distribuição binomial e faça um gráfico.

·  n é o número de pessoas: n = 3

·  X é o número de pessoas com Rh+ na amostra

·  p é a probabilidade de Rh+: p = 0,85

·  q é a probabilidade de Rh-: q = 0,15.

 

Cálculos intermediários para obter a distribuição binomial

Para construir a tabela de distribuição binomial, some probabilidades de eventos que levam ao mesmo valor de X. A distribuição é dada na tabela a seguir. 

💡  Resposta:

Distribuição de probabilidades do número de pessoas com Rh+, numa amostra de três pessoas

Distribuição de probabilidades do número de pessoas com Rh+, numa amostra de três pessoas

      Exemplo 5: No caso de organismos diploides, os gametas têm distribuição binomial, uma vez que apenas dois resultados são possíveis em cada tentativa. Suponha que, em uma população parental de moscas das frutas, a frequência de alelos para o fracasso (F) de um inseticida usado no combate de moscas seja ½ e a frequência de alelos para sucesso (S) seja ½· Vamos supor que apenas três zigotos sobreviveram quando o inseticida foi aplicado.

 a) Nestas condições, qual é a probabilidade de que os três sejam homozigotos FF?

 b) qual é a probabilidade de que cada um dos três zigotos tenham genótipos diferentes? Em outras palavras, qual é a probabilidade de obter FF, FS, SS?

💡  Resposta:

 a)       n = 2N gametas na amostra = 6 

            x = número de gametas F na amostra = 6

b)       Probabilidade de que três gametas tenham o alelo F e três tenham o alelo S.

Bit a Bit: Como um Jogo de Moedas Explica o Mundo Digital e Estatístico

Quando se lança uma moeda uma única vez, o resultado — cara ou coroa — é determinado pelo acaso. O resultado desse lançamento é, portanto, uma variável aleatória. Como existem apenas dois resultados possíveis, dizemos que essa variável é binária. A probabilidade de ocorrer cara é p = 1/2 e a de ocorrer coroa é q = 1/2.

Agora, imagine que a moeda seja lançada muitas e muitas vezes, digamos, n vezes. Nessas jogadas, ocorrerá um certo número de caras, que indicaremos por X. Essa nova variável, o número de caras em n lançamentos, também é aleatória, pois o resultado de cada jogada é imprevisível e fruto do acaso.

Podemos calcular a probabilidade de que, em n jogadas, X seja igual a 0, 1, 2, ..., n. Estamos, então, diante de uma distribuição de probabilidades, pois cada possível valor de X está associado a determinada probabilidade. Essa distribuição é chamada de binomial, porque cada lançamento da moeda tem apenas dois resultados possíveis: cara ou coroa.

📢  Propriedades essenciais

🔺A probabilidade de X assumir qualquer valor possível é sempre maior ou igual a zero — não pode ser negativa.

🔺A soma das probabilidades de todos os valores possíveis de X é igual a 1.

Para estudar a distribuição da variável aleatória X, vamos definir que em cada lançamento:

 🔸 Se sair coroa, atribuímos X = 0.

 🔸 Se sair cara, atribuímos X = 1.

Fica então fácil entender o conceito de dígito binário ou binary digit, que deu origem ao termo bit — indicando duas possibilidades: sim ou não, ligado ou desligado.

Vamos voltar ao jogo de moedas e considerar, primeiramente, n = 1 lançamento. Os valores que a variável X pode assumir e suas respectivas probabilidades estão na Tabela 1.

Tabela 1

Distribuição binomial com n = 1 e p = ½

Agora, consideremos que a moeda seja lançada n = 2 vezes. Os valores possíveis de X e suas probabilidades estão na Tabela 2.

Tabela 2

 Distribuição binomial com n = 2 e p = ½

Se a moeda for lançada n = 3 vezes, temos a Tabela 3.

                                             Tabela 3

                    Distribuição binomial com n = 3 e p = ½

Observe as tabelas 1, 2 e 3:

🔸 Se n = 1, X pode ser 0 ou 1.

🔸 Se n = 2, X pode ser 0, 1 ou 2.

🔸 Se n = 3, X pode ser 0, 1, 2 ou 3.

É natural concluir que, para um valor fixado de n, a variável aleatória X pode assumir qualquer valor inteiro entre 0 e n, inclusive.

As tabelas também mostram a probabilidade correspondente a cada valor de X. Por extensão, podemos dizer que, conhecido o valor de n, é possível calcular a probabilidade de X assumir qualquer valor inteiro de 0 a n.

Vamos aceitar, sem demonstração, que a probabilidade de X assumir um valor específico x é dada pela fórmula da distribuição binomial:

onde:

       🔸 é o coeficiente binomial.

        🔸 p é a probabilidade de sucesso (por exemplo, sair cara).

       🔸 q=1−p é a probabilidade de fracasso (por exemplo, sair coroa).

Para praticar, vamos usar n = 4. Quando uma moeda é lançada 4 vezes, podem ocorrer 0, 1, 2, 3 ou 4 caras. Usando a fórmula, calculamos as probabilidades para cada valor de X e organizamos os resultados na Tabela 4.

Tabela 4

Distribuição binomial com n = 4 e p = ½

 

📢  Características da Distribuição Binomial

🔸  São n eventos idênticos (também chamados ensaios ou tentativas).

🔸  Cada evento tem dois resultados possíveis: “sucesso” (X = 1) e “fracasso” (X = 0).

🔸 A probabilidade de sucesso em cada evento é constante e igual a p.

🔸 Os eventos são independentes: o resultado de um não afeta os demais.

🔸 A variável aleatória X representa o número de sucessos em n eventos.

              📢          Parâmetros da Distribuição Binomial

1.            n: número de eventos ou tentativas (exemplo: lançar uma moeda 10 vezes).

2.           p: probabilidade de sucesso em cada tentativa (exemplo: sair cara em um lançamento).

                                     Importante lembrar

✅  n é o número de tentativas

✅ x é o número de sucessos

✅ p é a probabilidade de sucesso

✅! indica fatorial, utilizado em cálculos de análise combinatória.                    

 Convém observar que: