Uma doutoranda da Unicamp, que não conheço pessoalmente, me apontou gentilmente, por e-mail, o que ela considerou um “pequeno erro de cálculo” em meu livro, Análise de variância: o resultado do coeficiente de variação (CV), que consta na página 47, estaria errado. Claro, busquei rapidamente o texto e me pus na frente do computador.
Tabela de análise de variância
Em
qualidade, não é usual proceder a uma análise de variância. Calculam-se médias,
desvios padrões, gráficos de controle. Então a doutoranda, que é da área de
qualidade, calculou, como sempre fez, as médias e os desvios padrões do exemplo
dado. Obteve:
Médias e desvios padrões segundo os tratamentos
Está
tudo bem até aqui. Mas depois, estudando no meu livro Análise de
variância, a doutoranda leu: Pode existir interesse em relacionar o desvio
padrão com a média, para se ter ideia da grandeza da dispersão em relação à
grandeza da média. Por definição, coeficiente de variação, que se
indica por CV, é a razão entre o desvio padrão e a média dos dados,
isto é
Havia,
também, esta informação: na análise de variância, o desvio padrão é dado pela
raiz quadrada do quadrado médio do resíduo. Reconheço que o que está escrito no
livro não é suficiente para esclarecer um aluno. De qualquer forma,
ali está apresentado o valor correto para do coeficiente de variação para o
exemplo dado acima:
Mas
vamos aos fatos. A análise de variância não é técnica comum entre pesquisadores
da área de qualidade. Então a doutoranda NÃO tinha o cálculo do quadrado médio
do resíduo (QMR). O coeficiente de variação foi calculado
fazendo a média das médias e a média dos desvios padrões, com base
nos resultados apresentados na tabela de médias e desvios padrões. Está errado:
Para explicar isso, resolvi recorrer ao Dr. Math (Doctor Schwa, The Math Forum http://mathforum.org/dr.math/) e apresentar um pouco de matemática.
Vamos voltar ao coeficiente de variação. Na tabela apresentada
anteriormente, de médias e desvios padrões, deveriam ter sido apresentadas as
variâncias de cada grupo, além de médias e os desvios padrões.
Médias, variâncias e desvios padrões segundo os tratamentos
Demorei
muito para entender que a fórmula, como está na definição dada em meu
livro, Análise de variância, e é a comumente apresentada nos livros
didáticos de estatística, pode levar a erro. No livro está escrito:
Por
definição, coeficiente de variação, que se indica por CV,
é a razão entre o desvio padrão e a média dos dados, isto é
A
fórmula está correta desde que em análise haja uma única variável em um só
grupo. Nos experimentos ou ensaios completamente randômicos, uma variável é
observada em k grupos. Se for calculada a média e o desvio
padrão de cada grupo, o coeficiente de variação (geral) será dado pela divisão
da raiz quadrada do quadrado médio do resíduo da análise de variância pela
média geral. O quadrado médio do resíduo (QMR), desde que todos os
grupos tenham r repetições, é
é a variância do i-ésimo
tratamento e o QMR é a média das variâncias de cada grupo.
Procure o livro em http://www.saraiva.com.br/
analise-de-variancia-anova-1100479.html













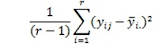

1 comment:
Olá Sonia, parabéns pelo blog e livros! Seu material tem sido de grande ajuda para meu aprendizado.
Desculpe-me por tomar seu tempo, mas estou lhe escrevendo por que estou com dificuldade de encontrar material detalhado sobre o Teste POST-HOC de Tukey HSD que faça a análise com base nas letras a,b,c etc. Estou tentando entender a lógica para identificar as significâncias no formato da tabela abaixo, mas não encontrei nenhum livro ou material que explique. Você tem algum livro ou material para indicar que explique como analisar os dados neste método de letras?
9,800 15,400 17,600
15 a b b
20 a b↓ b
25 a bc c
Obrigado,
Geucimar
Post a Comment