Para melhor conhecer a distribuição hipergeométrica,
vamos voltar ao exemplo dado na postagem anterior.
PROBLEMA: Uma caixa contém 20 bolas vermelhas e 20 bolas azuis. Quatro bolas são retiradas da caixa ao acaso. Seja X1 o número de bolas vermelhas que podem ser retiradas da caixa. Vamos fazer, consecutivamente, X1 = 0, 1, 2, 3, 4. Calcule as respectivas probabilidades. Você terá a distribuição hipergeométrica para N = 40, N1 = 20, N2 = 20 e n = 4. Organize os resultados em uma tabela e em um gráfico.
SOLUÇÃO:
É dada a fórmula:
Comece fazendo, nessa fórmula, x1 = 0. Então:
Tabela 1. Distribuição
hipergeométrica: N1= N2=20, n= 4
|
X1 |
P(X1) |
|
0 |
0,05301 |
|
1 |
0,24948 |
|
2 |
0,39501 |
|
3 |
0,24948 |
|
4 |
0,05301 |
|
Total |
1 |
Gráfico 1. Distribuição
hipergeométrica N1= N2= 20 e n= 4
A distribuição é
simétrica. Vamos ver então uma distribuição hipergeométrica assimétrica.
PROBLEMA: Uma caixa contém 20 bolas vermelhas e quatro bolas azuis. Quatro bolas são retiradas da caixa ao acaso. Faça X1 indicar o número de bolas vermelhas retiradas. Os valores possíveis são X1 = 0, 1, 2, 3, 4. Calcule a probabilidade para cada um desses valores possíveis de X1 e você terá a distribuição hipergeométrica para n1 = 20 e n2 = 4 e n = 4. Organize os resultados em uma tabela e em um gráfico.
É dada a fórmula:
Fazendo X1 = 0, 1, 2, 3 e 4
consecutivamente, você obtém as respectivas probabilidades. Os resultados estão na
Tabela 2 e no Gráfico 2. Note que a distribuição é assimétrica.
Tabela 2. Distribuição hipergeométrica N1=20, N2=4 e n=4
Gráfico 2. Distribuição
hipergeométrica: N1=20, N2=4 e n=4
Para bem entender a distribuição hipergeométrica, vamos ver outro exemplo. Mas saiba que os resultados de problemas como os apresentados aqui podem ser apresentados em uma tabela 2 x 2. Veja a tabela 3, que apresenta os resultados de uma distribuição hipergeométrica.
Tabela 3.
Apresentação tabular da distribuição hipergeométrica
Vamos limitar nossa apresentação das possíveis
distribuições hipergeométricas a partir de um exemplo de Fisher, o famoso
estatístico que propôs, a partir da distribuição hipergeométrica, o teste
exato de Fisher. Veja a Tabela 4. A distribuição está no Gráfico 3.
Os totais marginais são fixos. A tabela tem 1 grau de
liberdade, isto é, mudando o valor de uma célula, mudam os valores de todas as
outras. Vamos então estudar a distribuição para número de mortos igual a zero,
1, 2 e 3. Então:
Veja agora a Tabela 5 e a respectiva distribuição, que está
no Gráfico 4. O tamanho dos grupos foi modificado, mas foram mantidos o
tamanho da população (6) e tamanho da amostra (3). Vamos então estudar a
distribuição para xi = 1, 2 e 3. Note que xi não
pode ser igual a 4, porque
a amostra é de tamanho 3, nem igual a zero, porque só há dois controles. Então,
uma amostra de 3 contém, necessariamente, um elemento tratado.
Gráfico 4. Distribuição hipergeométrica N1= 4, N2= 2 n= 3
Observe agora a Tabela 6 e
a respectiva distribuição, que está no Gráfico 5. O tamanho dos grupos foi
modificado, mas mantidos o tamanho da população (6) e o tamanho da amostra (3).
Vamos então estudar a distribuição para xi
= 2 e 3. Note que outros valores de xi
não são possíveis.
Tabela 6. Distribuição hipergeométrica N1 = 5, N2 = 1, n = 3
Gráfico 5. Distribuição hipergeométrica N1= 4, N2= 2 n= 3
Como pode ser entendido
destes últimos exemplos, mantendo fixos os tamanhos da população e da amostra,
mas fazendo variar o tamanho dos grupos, mudam as probabilidades associadas às
diferentes células da tabela.
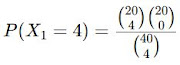
2 comments:
Bom dia professora. Estava fazendo um exercício sobre o teste de Scheffé do livro e estou com uma dúvida: no livro, o contraste de médias é:
L= 21 + 8 +10 + 29 + 13 - 5 * 2 = 91
o resultado desse cálculo não seria 71?
Sem dúvida, Marcelle, o resultado dessa soma é 71. Mas como você não cita o contexto, não sei dizer se é na soma ou se seria em algum outro ponto, na definição do contraste, que a soma deu errado. Mas que você apontou um erro, não tenho dúvida. Obrigada.
Post a Comment