A discussão aqui apresentada sobre operações com matrizes não é rigorosa, mas esperamos que suficiente para usuários.
1. Soma de matrizes
Para somar duas matrizes, A e B, some os
elementos que estão em posições correspondentes.
Exemplo
São dadas duas matrizes, A e B. Veja como se faz a soma.
Formalizando: " A soma de duas matrizes de igual ordem A=[aij] e B=[bij] é uma matriz C da mesma ordem de A e B e seus elementos são obtidos pela soma aij +bij.""
Importante: só podem ser somadas matrizes de mesmo tamanho. Não se pode somar uma matriz 3 x 2 com uma matriz 2 x 3.
2. Subtração de matrizes
Para subtrair matrizes, isto é, subtrair B de A, proceda à subtração dos elementos que ocupam posições correspondentes.
Exemplo
São dadas as mesmas duas matrizes de
mesma ordem, A e B. Veja como se subtrai B de A.
3. Multiplicação de
matrizes
4.3.1.
Multiplicação de matriz por um escalar
É
fácil multiplicar uma matriz por um número real k. Por exemplo, para multiplicar a matriz M
por 2,
isto é, para obter 2 x M multiplique
cada elemento da matriz M por 2:
Então:
Generalizando: para multiplicar uma matriz M
de ordem m x n por um número real k, é
preciso multiplicar k por cada um dos
elementos de M.
4.3.2.
Multiplicação de matrizes
Para multiplicar uma matriz A
por uma matriz B, é preciso
fazer o produto de linhas por colunas, ponto a ponto. Importante é que o número
de colunas em A seja igual ao número
de linhas em B. Se A é uma matriz m x n e B é uma matriz n x p, a matriz C resultante será m x p.
Exemplo
Sejam as matrizes A e B. A é matriz 2 x 3 e B é 3 x 2.
Exemplo
Sejam as matrizes A e B. A é uma matriz 2 x
3 e B
é 3 x 2.
A matriz C, resultante da multiplicação de uma matriz A, 2 x 3, por uma matriz B, 3 x 2, é uma matriz 2 x 2.
Para obter a matriz C:
1. Multiplique
os elementos da primeira linha de A
com os elementos correspondentes da primeira coluna de B:
2. Some
os produtos. O resultado é o primeiro elemento da primeira linha e primeira
coluna de C.
3. Multiplique
dos elementos da primeira linha de A
com os correspondentes da segunda coluna de B e some:
4. O
resultado é o primeiro elemento da primeira linha e segunda coluna de C.1.
5. Trabalhe agora com a segunda linha da matriz A e a primeira coluna da matriz B. O resultado é o elemento da segunda linha e primeira coluna da matriz C.
6. Finalmente, faça os cálculos com a segunda linha da matriz A e segunda coluna da matriz B. O resultado é o elemento da segunda linha e segunda coluna da matriz C.
7. Agora você tem o produto das matrizes A x B, ou seja, a matriz C.
Vamos definir mais formalmente a
multiplicação de matrizes. Considere uma matriz A de ordem m x n
e uma matriz B de ordem n x p.
O produto
Veja bem: você obtém o
elemento da i-ésima linha e j-ésima coluna da matriz
C, multiplicando todos os elementos da i-ésima
Exemplo
Dadas as matrizes A e B, calcule o produto delas.
Lembre-se de que, para que uma matriz A possa ser multiplicada por uma matriz B, o número de colunas de A deve ser igual ao número de linhas de B. Observe: o número de colunas de A é igual ao número de linhas de B, isto é, 2. Então C, que é o produto de A por B, é uma matriz 2 x 2.
Exemplo
Dadas as matrizes M e N, o produto
Observe: o número de colunas de M é 2, diferente do número de linhas de N. Então o produto dessas duas matrizes não é definido.
4.3.3.
Propriedades da multiplicação de matrizes
1ª propriedade
Uma matriz A pode ser multiplicada por uma matriz B somente se o número de colunas de A for igual ao número de linhas de B. O resultado da multiplicação terá o número de linhas da primeira matriz e o número de colunas da segunda matriz.
2ª propriedade
A multiplicação de matrizes
não é comutativa. Mesmo que seja
possível multiplicar A por B e B por A, os produtos podem ser
diferentes e de ordens diferentes.
1. Se A for de ordem n
x m e B for de ordem m x n,
Exemplo
Vimos que:
Vamos obter
Verifique:
2. Ainda que A e B sejam matrizes quadradas, as matrizes resultantes da
multiplicação de A e de B não são necessariamente iguais.
Exemplo
Dadas as matrizes A e B, verifique que:
3ª propriedade
Um vetor linha pós-multiplicado por um vetor coluna é um
escalar.
Exemplo
São dados os vetores
O produto deles é um escalar:
4ª propriedade
Um vetor coluna pós-multiplicado por um vetor linha é uma
matriz.
Exemplo
São dados os vetores
O produto deles é uma matriz de ordem 3 x 3:





















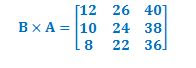





No comments:
Post a Comment