Sonia Vieira: Regressão linear múltipla no SPSS

A análise de regressão permite estabelecer um modelo para a relação entre duas ou mais variáveis. Uma regressão é, portanto, uma função que permite fazer previsões sobre uma variável – que chamaremos de variável resposta (dependente) – com base nas informações obtidas de outras variáveis – que chamaremos de variáveis explicativas, explanatórias ou preditoras (independentes).

A regressão linear simples é dita linear porque o modelo ajustado é uma reta, e simples porque há apenas uma variável explicativa. A regressão linear simples é definida pelo modelo

Nesse modelo, os pares de variáveis Y_i e X_i (i=1,2,...,n) são a variável resposta e a variável explicativa, respectivamente; b₀ e b₁ são parâmetros a serem estimados para um conjunto de dados e e_i(i=1,2,...,n) são erros aleatórios.

Se você tiver, por exemplo, um conjunto de dados de peso e altura de jovens que se apresentaram para o serviço militar e considerar que peso é função linear da altura, pode ajustar uma reta aos dados, para obter as estimativas b₀e b₁dos parâmetros b₀e b_1.

O termo b₀é o coeficiente linear, também conhecido como intercepto (em inglês, intercept) e o termo b₁é o coeficiente angular, também conhecido como inclinação (em inglês, slope). A melhor reta ajustada aos dados (melhor, no sentido que tem as propriedades estatísticas desejáveis) recebe o nome de reta de regressão. Muitos autores referem-se à reta de regressão como reta de mínimos quadrados porque esse é o método estatístico aplicado para chegar às fórmulas que permitem calcular as estimativas.

A regressão linear múltipla (multiple linear regression) é uma técnica estatística que usa diversas variáveis explicativas para prever a variável resposta. Logo, a regressão linear múltipla estabelece o modelo para uma relação linear entre a variável resposta (dependente) e diversas variáveis explicativas (independentes).

A regressão linear múltipla é definida pelo modelo

Nessa fórmula, Y_i (i =1, 2,...,n) são as n observações da variável resposta (dependente) e X_i₁, X_i₂,...,X_ik são as n observações das k variáveis explicativas (independentes).

Ainda, b₀é coeficiente linear (intercepto) e b₁, b₂,...,b_ksão coeficientes angulares para cada variável explicativa (slopes); e_isão termos de erros do modelo.

Para ajustar um modelo de regressão linear múltipla a um conjunto de dados, é preciso pressupor que:

· A variável resposta (dependente) seja contínua.
· Exista uma relação linear entre a variável resposta e cada uma das variáveis explicativas.
· As variáveis-resposta, selecionadas ao acaso na população, sejam independentes.
· Os resíduos tenham distribuição normal de média zero e variância s².

Vamos mostrar aqui, por meio de um exemplo, como se ajusta uma regressão linear múltipla a um conjunto de dados, usando o SPSS (um software estatístico chamado Statistical Package for Social Sciences). Daremos também breves explicações de como interpretar os dados em uma próxima postagem.

Exemplo

Imagine uma amostra aleatória de 12 crianças que estão em uma clínica. O peso, a altura e a idade dessas crianças são dados abaixo, já na forma como você deve colocar em arquivo. O peso (weight) é dado em libras, a altura (height) em pés e a idade (age) em anos completos. Você quer estudar o peso em função da altura e da idade.

As etapas dadas em seguida mostram como analisar dados usando regressão linear múltipla no SPSS quando nenhuma das pressuposições foi violada. No final dessas etapas, mostramos os resultados da sua regressão múltipla. Seus dados devem estar no arquivo.

Clique Analisar, Regressão, Linear no menu principal.

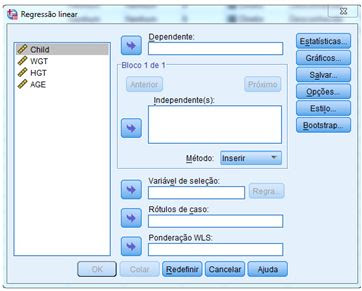
Você será apresentado à caixa de diálogo:

Transfira a variável dependente peso (WGT) para a caixa “dependente” e as variáveis independentes altura (HGT) e idade (AGE) para a caixa “independente” usando o botão