Antes de tratar intervalo de confiança, é
importante lembrar dois conceitos básicos: estimativa por ponto e estimativa
por intervalo. Toda estatística amostral é, por definição, uma estimativa
por ponto de algum parâmetro populacional. Por exemplo, imagine que você
mediu a altura de 10 homens adultos de uma região e encontrou média de 170 cm.
Esse valor é uma estimativa por ponto da altura média dos homens adultos
daquela região.
Uma estimativa
por intervalo busca fornecer um intervalo de valores dentro do qual
está, com certa confiança, o verdadeiro valor do parâmetro. Continuando o
exemplo, após cálculos com a mesma amostra, você poderia afirmar que tem 95% de
confiança que a média populacional de altura está entre 165 cm e 175 cm. Isso
amplia a informação, pois em vez de um único número, você oferece uma faixa com
chance de conter o verdadeiro valor.
Exemplo
Comparação de grupos com ANOVA e intervalos de
confiança
Agora, vamos aplicar o conceito em uma situação real de análise estatística, onde são comparadas as médias de quatro grupos, cada um com cinco repetições. Suponha os seguintes dados fictícios, fáceis de digitar, apresentados na Tabela 1. As médias estão no rodapé da tabela.
Tabela 1
Dados (fictícios) para comparação de grupos
⚠️Pergunta: As diferenças entre as médias dos grupos são grandes o suficiente para concluir que os grupos são estatisticamente diferentes?Para responder, utilizamos a análise de variância (ANOVA), que testa a hipótese:
· H₀: todas as médias populacionais são iguais.
· H₁: pelo menos uma média de grupo é diferente das demais.
A análise de variância (ANOVA) produz uma estatística F que indica se há
diferença global entre os grupos. Se F for significante, é comum seguir com comparações
duas a duas (pairwise comparisons), em geral usando o teste de
Tukey.
Tabela 2
Análise de variância
No caso do exemplo, o valor calculado de F
é altamente significante
(comparado com o valor crítico de F, para 3 e 16 graus de liberdade, no nível
de significância 0,05, que é 3,24). Portanto, há pelo menos
uma média de grupo é diferente das demais. Mas em lugar de comparar médias duas
a duas usando o teste de Tukey, vamos calcular os intervalos de confiança das diferenças entre médias que
também indicam quais grupos realmente se diferenciam.
Intervalos simultâneos de confiança com o
teste de Tukey
O teste de Tukey permite calcular intervalos de
confiança simultâneos para todas as diferenças entre as médias. Esse método
é conservador, mantendo o controle sobre o erro tipo I quando se fazem
múltiplas comparações.
Para grupos de mesmo tamanho (como no exemplo), os intervalos para diferenças de médias são dados por:
Onde:
· qα,k,gl é o valor da tabela de Tukey, dado o número de grupos (k), graus
de liberdade do erro (gl) e nível de significância (α, por exemplo,
0,05);
· QMR: quadrado médio do resíduo da ANOVA;
· r: número de repetições por grupo.
No caso do exemplo:
🔺 Valor de q de Tukey
Para α=0,05, k=4 , gl = 16, da tabela de
Tukey:
q=4,05
🔺 Cálculo
do erro padrão conjunto (EP)
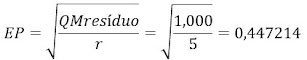
Tabela 3
Diferenças de médias
🔺 Intervalos de confiança (95%) para as diferenças
Tabela 5
Intervalos de confiança simultâneos 95% (Tukey)
Um gráfico com médias e desvios padrão pode ilustrar a comparação entre grupos.







No comments:
Post a Comment