O problema ou paradoxo de Monty Hall é
aparentemente fácil, mas, na realidade, é um problema de probabilidade de
difícil solução. Só para deixar você tranquilo – estatísticos profissionais já
erraram – e para ter certeza de que a solução dada aqui, hoje bem conhecida, é
a correta, fizeram até simulações.
Mas vamos primeiro à história do
problema. Na década de 70 havia um programa de auditório apresentado por Monty
Hall na ABC, rede de televisão
nos Estados Unidos da América. O quadro de maior sucesso era Let’s Make a
Deal! O apresentador, Monty Hall, convidava alguém da platéia para ir até o
palco e escolher uma de três portas que ali estavam.
Veja bem: eram três portas. Atrás de uma delas havia
um carro; atrás de cada uma das outras duas, havia uma cabra. O apresentador
sabia o que estava atrás de cada porta, mas seu convidado não. De qualquer
forma, o convidado escolhia uma das portas ao acaso, sabendo que receberia como
prêmio o que estava atrás dela.
Para resolver o problema, vamos construir o espaço
dos eventos possíveis. São três portas (porta nº 1; porta nº 2; porta nº 3) Há
três possibilidades de o apresentador arranjar carro e cabras, que
denominaremos A, B e C. Veja a tabela abaixo.
Arranjo (posição
de carro e cabras)
|
Porta escolhida
|
||
Porta 1
|
Porta 2
|
Porta 3
|
|
A
|
Carro
|
Cabra
|
Cabra
|
B
|
Cabra
|
Carro
|
Cabra
|
C
|
Cabra
|
Cabra
|
Carro
|
Qualquer que
seja o arranjo do carro e das cabras – A, B ou C –, a probabilidade de uma
pessoa ganhar o carro é 1/3, se escolher uma porta ao acaso sem saber o que há detrás
dela.
O convidado
fazia então sua escolha. Feita a escolha, o apresentador abria outra porta –
que não a indicada pela pessoa convidada – e mostrava que havia ali uma cabra.
Veja bem: qualquer porta que a pessoa tenha escolhido, sempre haverá outra
porta com uma cabra atrás. O apresentador então perguntava:
Quer trocar a porta que você
escolheu e ainda está fechada, pela outra porta, que também está fechada?
Se o convidado trocar a porta que escolheu tem
probabilidade 2/3 de ganhar.
Se não
mudar a opção, a probabilidade de ganhar o carro é 1/3. Difícil de engolir?
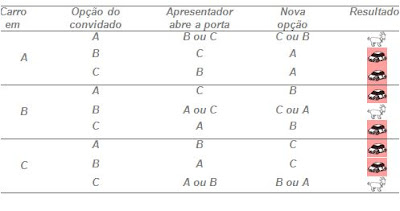
Mas vamos lá: veja
a tabela dada anteriormente. Há três arranjos possíveis para os prêmios: A, B,
C. Veja o arranjo A:
As opções
do convidado eram três. Escolher:
·
Porta 1: o apresentador
abriria a Porta 2 ou a 3; trocar significa ganhar
uma cabra.
·
Porta 2, o
apresentador abriria a Porta 3; trocar significa ganhar o carro.
·
Porta 3, o
apresentador abriria a Porta 2; trocar significa ganhar o carro.
Se a
ordem do arranjo for A, a pessoa ganha (se trocar) em duas das três opções. Veja
a tabela dada em seguida. Acontece o mesmo se a ordem dos arranjos for B ou C.
Esta resposta foi
dada por Marilyn vos Savant, de QI sabidamente alto, escritora e colunista da
revista Parade dos Estados
Unidos da América. Na revista, Marilyn vos Savant
responde a perguntas de seus leitores sobre matemática e ciência avançada. Mas
a solução não foi aceita pacificamente. Muitos probabilistas duvidaram da
resposta, mas acabaram vencidos.
Referências
1. MLODINOW, L. O Andar do Bêbado. Rio de
Janeiro Zahar. 2009. Tradução de Diego Alfaro.
2. ALIAGA, M. e GUNDERSON, B. Interactive Statistics. New
Jersey, Prentice Hall, 2 ed. 2003.


No comments:
Post a Comment