Quando pensamos em uma distribuição de probabilidades, é comum imaginarmos a distribuição normal também chamada de distribuição de Gauss — simétrica, com uma curva em forma de sino e conhecida por sua aparência suave e regular. Veja a Figura 1. Essa distribuição é classificada como mesocúrtica – e o que é a curtose vamos ver neste post.
O que são as caudas de uma distribuição?
A curtose está relacionada às caudas das
distribuições. Em um gráfico de uma distribuição de probabilidades, as caudas
são as extremidades à direita e à esquerda do pico central. Elas representam a
frequência com que ocorrem valores extremos — poucos ou muitos. A curtose se
refere ao grau em que os dados estão concentrados nessas regiões extremas. Em
outras palavras, trata-se de quanto da variabilidade da variável está nas
caudas da distribuição.
Tomando a distribuição normal como referência, podemos comparar outras
distribuições a ela, observando se há mais ou menos dados nas caudas.
Três tipos principais de curtose
1.
Mesocúrtica: é o caso da própria distribuição normal, cuja
quantidade de dados nas caudas é considerada “normal” ou média. Algumas
distribuições, como a binomial com probabilidade próxima de ½ e tamanho de
amostra grande, também se aproximam desse padrão.
2.
Leptocúrtica: distribuições com caudas mais “pesadas” ou
espessas que as da normal. Isso indica uma maior concentração de valores
extremos, o que pode significar maior presença de outliers. Um exemplo típico é
a distribuição t de Student.
3. Platicúrtica: distribuições com caudas mais “leves” ou
finas, ou até sem caudas marcadas. Nesse caso, há menos valores extremos, e os
dados tendem a se concentrar mais em torno da média. A distribuição uniforme é
um exemplo de platicurtose.
A origem do
conceito
O conceito de curtose foi introduzido por Karl Pearson, que o associou à ideia
de “achatamento” da curva de uma distribuição. Segundo essa interpretação
inicial, distribuições com picos mais baixos seriam platicúrticas, e as com
picos mais altos e estreitos seriam leptocúrticas.
No entanto, essa visão não é a mais precisa. A curtose está mais relacionada ao
comportamento das caudas — ou seja, ao que ocorre nos extremos — do que à forma
do pico. O pico da curva contribui muito pouco para o valor da curtose. Ainda
assim, é comum associar visualmente a leptocurtose a curvas com picos agudos e
a platicurtose a curvas mais achatadas, o que pode levar a interpretações
equivocadas.
Como se mede a curtose?
Diferentemente da média e do desvio padrão, que
são expressos nas mesmas unidades dos dados, a curtose é uma medida adimensional.
Existem duas formas principais de expressá-la:
1. Curtose absoluta: também
chamada de coeficiente de curtose de Pearson, atribui valor 3 à
distribuição normal. Nesse caso, distribuições com curtose maior que 3 são classificadas
como leptocúrticas e aquelas com valor menor que 3 são classificadas como platicúrticas.
Em geral, é indicada por b2.
Onde · m4 é o quarto momento em relação à média, isto é, E[(X−μ4)]
· s é o desvio padrão (na definição, é o desvio padrão populacional).
2. Excesso de curtose:
conhecida como curtose de Fisher, é a forma mais utilizada atualmente,
inclusive na maioria dos softwares estatísticos. Aqui, a distribuição normal
tem curtose igual a zero. Então valores positivos indicam leptocurtose e
valores negativos, platicurtose. Em geral, é indicada por g.
É claro que uma distribuição pode ser considerada mesocúrtica mesmo que o coeficiente de curtose de Fisher esteja apenas em torno de zero, não precisa ser exatamente zero. Um teste é possível. Mas importante é esclarecer sempre qual definição está sendo adotada ao apresentar o valor da curtose.
Note que para calcular os coeficientes de curtose, foi usada a variância dividida por n, mas é comum usar a variância amostral, dividida por n - 1.
Curtose em amostras pequenas
Em amostras pequenas, o valor calculado da curtose pode superestimar o valor
real da população. Isso ocorre porque a fórmula da curtose depende de momentos
estatísticos que são especialmente sensíveis a valores extremos. Por essa
razão, é comum aplicar uma correção para viés, que os softwares
estatísticos costumam realizar automaticamente. Essa correção busca tornar a
estimativa mais precisa, mesmo com poucos dados. A fórmula é dada por
Em resumo
1. A curtose descreve como os dados se distribuem nas caudas de uma distribuição.
2. A distribuição normal serve como referência.
3. Leptocurtose indica maior presença de valores extremos; platicurtose indica menor presença.
4. Curtose não mede o pico da curva, embora essa associação visual ainda seja comum.
5. Há duas formas principais de expressar a curtose: com base absoluta (valor 3 para a normal) ou com base no excesso (valor 0 para a normal).
6. Em amostras pequenas, é necessário aplicar uma correção para evitar distorções.
Exemplos de cálculo da curtose
Exemplo 1
Considere os seguintes valores: 1, 3, 6, 10.
Vamos calcular média, variância, desvio padrão e curtose.
Tabela 1: Cálculos intermediários para para cálculo curtose
Cálculo da curtose absoluta
Para esse conjunto de valores, a curtose absoluta é menor que 3 e a curtose em excesso é negativa, indicando uma distribuição platicúrtica, ou seja, com caudas mais leves do que as da normal.
Cálculo da curtose com correção de viés
Tabela 2: Cálculos intermediários para
curtose com correção de viés
Fazendo os cálculos pelo
EXCEL (use CURT),você encontra -0,76843.
Então: b2 =01,6975
<3; curtose em excesso g = -2,045 < 0; curtose ajustada para
tamanho da amostra -0,768 < 0. A distribuição é platicúrtica. Apresenta curtose negativa
baixa, indicando que tem menos valores discrepantes do que uma distribuição
normal.
Calcule média, variância, desvio padrão e curtose para os dados apresentados na Tabela 3. Faça um histograma.
Tabela 3: Dados
Cálculos usando
o Excel
Você
também pode usar uma calculadora online para obter a curtose. (kurtosis
calculator)
Curtose:
2.9804
The distribution
is leptokurtic. It has a high positive kurtosis, indicating that it is very peaked and has a relatively large number of outliers.
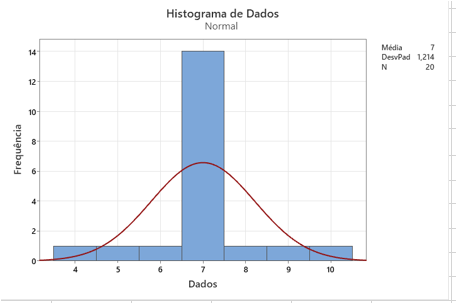
Calcule média, variância, desvio padrão e curtose para os dados apresentados na Tabela 4. Faça um histograma.
Tabela 4: Dados



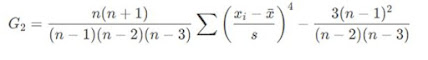

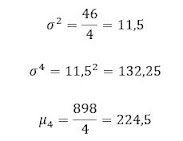







2 comments:
Obrigado pelo conteúdo. Vários posts do seu blog têm me ajudado muito nos estudos :)
Felipe.
Post a Comment