Distribuição Normal: Por que é tão comum?
Uma variável aleatória contínua pode
assumir qualquer valor dentro de um dado intervalo. Existe, portanto, um número
infinito de valores possíveis considerando dois valores. Por exemplo, altura de
pessoas é uma variável contínua. Entre dois valores possíveis quaisquer – como
1,70 m e 1,80 m – podem ser encontrados infinitos valores.
A distribuição dos valores possíveis de uma variável contínua é descrita por uma função de densidade de probabilidade (ou simplesmente função de densidade). Vamos começar entendendo o que é distribuição. E – para isso – vamos ver a distribuição normal.
Distribuição normal
Mas... Por que a distribuição normal aparece tanto?
A curva normal já era conhecida há
bastante tempo quando Gauss, o grande matemático e astrônomo do século XIX,
fazendo medições em seus estudos de astronomia, constatou que:
🔹 Quando são feitas várias medições, o
valor mais provável para a resposta real é a média das medições.
🔹 Erros pequenos são mais prováveis do
que erros grandes.
🔹Para qualquer número E, ter erro +E é
tão provável quanto ter erro -E.
A partir dessas suposições simples,
Gauss criou a “fórmula” (função de densidade de probabilidade) da distribuição
normal e usou essa distribuição para estudar erros de medição.
Vamos olhar primeiro o aspecto gráfico
da distribuição. É uma curva em forma de sino, simétrica em torno da média. A
probabilidade de a variável aleatória assumir qualquer valor dentro de
determinado intervalo é dada pela altura da curva. Isto significa que, se
estivermos estudando erros de medição, a probabilidade de erros positivos é
igual à probabilidade de erros negativos.
Ainda, erros pequenos (próximos da
média) são mais prováveis do que erros grandes (longe da média). Isso dá a
configuração da curva, mostrada na figura.
Gráfico da curva normal
Para mais bem compreender a questão dos
erros, um exemplo excelente é dado por Mlodinov:
Imagine que vamos fazer 150 pães um a
um, seguindo uma receita que produz pães com 500 gramas. Por simples acaso,
poderemos colocar mais, ou menos, farinha e/ou leite e/ou açúcar em alguns
pães. O forno pode estar mais quente, ou menos quente. Pode haver variações de
umidade no ar e temperatura ambiente.
O fato é que, no final, teremos alguns
pães com mais do que 500 gramas, outros com menos e a maioria com pesos muito
próximos de 500 gramas.
O peso de nossos pães irá variar de
acordo com a distribuição normal. Por quê? Porque sobre o peso de nossos pães
atuou grande número de variáveis aleatórias independentes – algumas atuaram
para aumentar o peso, outras para diminuir. Cada variável tem efeito pequeno,
mas os efeitos se somam.
Distribuição de pesos dos
pães (imagem ilustrativa)
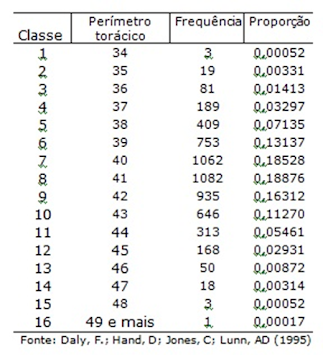
Foi Quetelet, matemático e sociólogo do
século XIX, quem achou que poderia aplicar a “lei dos erros” ao ser humano. Fez
medições em 5732 soldados escoceses. A tabela abaixo apresenta a distribuição
de frequências para o perímetro torácico.
Distribuição de frequências para o perímetro torácico de homens adultos, em polegadas
Observe a
tabela. Como a variável é contínua, pode ser mostrada por um histograma,
como mostrado na figura dada em seguida.
Histograma para a distribuição de frequências do perímetro torácico de homens adultos, em polegadas
Gráfico da distribuição
normal ajustada ao histograma
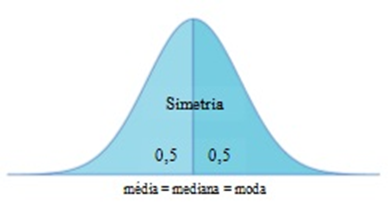
Características da distribuição normal
🔹 A área total sob a curva é 1.
🔹 Média, mediana e moda coincidem e
estão no centro da curva.
🔹 A curva é simétrica em torno da média:
50% dos valores estão abaixo da média, 50% acima.
Gráfico da distribuição
normal
A distribuição normal fica definida quando são dados dois parâmetros: a média
(representada pela letra grega μ) e o desvio padrão (σ). Mudando esses valores,
o aspecto da curva também muda.
Gráfico de três
distribuições normais
Conclusão
Medidas biológicas, industriais e erros
de medição são influenciadas por várias causas aleatórias. Por isso, a
distribuição normal aparece com frequência: ela é o resultado natural da soma
de pequenos efeitos aleatórios.
Referências
• Mlodinow, L. O andar do bêbado. Rio
de Janeiro: Zahar, 2009.
• Daly, F.;
Hand, D; Jones, C.; Lunn, A.D. Elements of Statistics. Addison Wesley, 1995.
•
https://onlinestatbook.com/2/normal_distribution/intro.html
•
https://onlinecourses.science.psu.edu/stat414/node/97
• https://stattrek.com/statistics/dictionary.aspx?definition=Probability-density-function
•
https://www.morris.umn.edu/~sungurea/introstat/history/Quetelet.html
Um exemplo simples
Leonard
Mlodinow explica que, ao assar 150 pães de 500g cada, pequenas variações nos
ingredientes, temperatura e umidade fazem com que o peso final varie de forma
aleatória. A maioria dos pães terá peso próximo de 500g, mas alguns serão mais
leves ou mais pesados.
✅ Conclusão
O
resultado é uma distribuição normal, pois muitos fatores aleatórios, atuando
independentemente, se somam.
O
resultado é uma distribuição normal, pois muitos fatores aleatórios, atuando
independentemente, se somam.
Veja mais em:
1. Mlodinow, L.
O andar do bêbado. Rio de Janeiro: Zahar, 2009.
2. Daly, F.;
Hand, D; Jones, C.; Lunn, A.D. Elements of Statistics. Addison Wesley, 1995.
3. https://onlinestatbook.com/2/normal_distribution/intro.html
4. https://onlinecourses.science.psu.edu/stat414/node/97
5. https://stattrek.com/statistics/dictionary.aspx?definition=Probability-density-function
6. https://www.morris.umn.edu/~sungurea/introstat/history/Quetelet.html








No comments:
Post a Comment