Paradigma

Toda discussão sobre História e Filosofia da Ciência perpassa, obrigatoriamente, nos trabalhos de Thomas Samuel Kuhn (1922-1996) que escreveu, entre outros, o livro

Nesse livro Kuhn explica que a prática científica se alterna entre períodos de “ciência normal” baseada em um paradigma e períodos de “revolução científica”, quando ocorre mudança de paradigma. Vamos discutir um pouco o significado desses termos.

Ciência normal significa fazer pesquisa baseada em conquistas científicas consagradas por determinada comunidade de cientistas. Como os cientistas estão comprometidos com a mesma maneira de fazer ciência, compartilham conhecimentos e modos de pensar. Então os pesquisadores aprendem como solucionar problemas em cursos, laboratórios, livros, manuais.

Enigmas e exemplos modelares A busca de solução para problemas, que Kuhn chamou de enigmas (em inglês, puzzles) é feito por meio das técnicas aprendidas nos exemplos modelares. Exemplos modelares (em inglês, exemplars) são as teorias que ditam as maneiras de pesquisar e dão as diretrizes para o trabalho científico.

Paradigma A pesquisa científica é orientada não apenas por teorias, mas por algo mais amplo, o paradigma. O que é paradigma?

Um conjunto de práticas que definem o comportamento dos cientistas durante determinado período de tempo.

Em determinada ciência você tem um paradigma quando sabe:

·  As verdades estabelecidas.

·  O que pode ser observado e examinado.

·  Quais são os tipos de questões que podem ser feitas e      pesquisadas para obter respostas sobre o assunto.

·  Como essas questões devem ser estruturadas.

·  Como os resultados das pesquisas científicas devem ser interpretados.

Kuhn conceituou paradigma em 1970, como

“um conjunto inteiro de crenças, valores, técnicas e tudo o mais que é compartilhado pelos membros de uma dada comunidade”.

Mais adiante Kuhn explicou que

 “paradigmas (são) soluções reais de enigmas que, usadas como modelos ou exemplos, podem ser tratados como se fossem regras explícitas e servir de base para a solução dos demais enigmas da ciência normal”.

A palavra paradigma criou, porém, vida própria. Aliás, Kuhn reconheceu que o conceito de paradigma escapou ao que ele próprio havia, de início, pensado.

Na tradução brasileira, o conceito de paradigma está expresso de maneira inadequada. Diz: “paradigmas são realizações (sic) científicas universalmente reconhecidas que, durante algum tempo, fornecem (sic) problemas e soluções modelares para uma comunidade de praticantes de uma ciência”.

Mudança de paradigma Não se muda de paradigma facilmente. Mudar de paradigma significa “adquirir” novos valores (um esforço) e apagar valores antigos (um esforço maior).

Mudar de paradigma não é mudar a técnica, mudar de texto, mudar de aparelho, como pensam alguns – mas ter uma “nova visão do mundo”, que possa ser compartilhada por toda uma comunidade de cientistas.

De qualquer forma, o sucesso de um paradigma depende do espaço que cria para que ocorram novas descobertas. Se uma conquista científica consegue dar solução para enigmas que não tinham solução satisfatória e for suficientemente original para atrair um grupo de bons cientistas a ponto de fazê-los abandonar o paradigma que conheciam, então você está diante de uma “revolução”.

Revolução científica ocorre quando há mudança de paradigma. A partir dessa mudança, a ciência evolui normalmente por certo tempo, dentro do novo paradigma. Mas é grande a força de um paradigma.

Na maior parte do tempo, a ciência exibe aderência ao paradigma. Os enigmas propostos para os cientistas resolverem estão circunscritos ao paradigma. Isto explicaria porque as revoluções científicas são raras.

Casos anômalos a ciência entra em crise quando é perdida a confiança na capacidade de o paradigma resolver casos discrepantes – os chamados “casos anômalos”.  Abre-se, então, caminho para uma revolução científica e para a construção de um novo paradigma.

Um exemplo de mudança de paradigma

Quando Christian Barnard substituiu o coração de um homem pelo coração de outro, mostrou ao mundo que uma pessoa pode viver com o coração de outra. Exibiu não apenas um resultado – mas rompeu um paradigma – não é preciso morrer quando o coração morre – e, em seu lugar, surgiu outro: órgãos podem ser transplantados.

Quando emerge um novo paradigma, a estrutura de toda a comunidade de cientistas é afetada. A aceitação de um novo paradigma – pelo menos por algum tempo – não se deve apenas aos recursos lógicos ou às evidências, experimentais ou não. A verdade é que cientistas que aderem a paradigmas diferentes têm visões diferentes do mesmo fenômeno (enquanto um vê o Sol girando em torno da Terra, o outro vê a Terra girando em torno do Sol)

Às vezes, chega ser impossível justificar a preferência de um cientista, ou de um grupo de cientistas, por determinado paradigma. Os que defendem o novo paradigma podem fazer propaganda e buscar novos adeptos pela conversão ou, simplesmente, esperar que os mais renitentes morram. Mas sempre haverá um tempo de acomodação. Por outro lado, há quem reconheça uma mudança de imediato.

Um reconhecimento de mudança de paradigma

O dentista Horace Wells (1815-1848) foi, indubitavelmente, quem primeiro usou anestesia em intervenções cirúrgicas. Na época, não foi reconhecida a importância da proposta. Mas – para demonstrar o efeito anestésico do éter sulfúrico – um aluno de Medicina de Harvard pediu ao professor de Cirurgia para anestesiar um paciente que seria submetido a uma amputação da perna no Hospital Geral de Massachussets. Isto foi feito em 1846. O paciente não demonstrou qualquer sinal de dor durante a operação, mas o professor John Warren Collins (1778-1856) se emocionou até as lágrimas. Reconheceu de imediato a mudança de rumo na história da cirurgia.

Mas quando isto acontece – a mudança de um paradigma – muita coisa também muda: a forma de um cientista ver o mundo; os critérios para selecionar os problemas importantes; as técnicas de pesquisa; a maneira de interpretar fenômenos; os critérios para avaliar teorias.

A atividade científica é crítica. Ser crítico implica admitir a probabilidade de erro. Então, dado que é possível que estejamos errados, é preciso procurar evidências para nossos juízos acerca dos fatos. Mais ainda, é preciso saber que o que é considerando evidência hoje pode não ser evidência amanhã. Afinal de contas, estamos circunscritos dentro de um tempo e de um lugar, para dizer o mínimo.

 Referências

1.    Kuhn, T. S. The Structure of scientific revolutions. 3ª ed. The University Chicago Press, 1996.

2.    Kuhn, T S. The Structure of Scientific Revolutions. 2nd ed., University of Chicago Press, Chicago & London, 1970, p.175.

3.    KATZ, J.  Experimentation with human beings. New York: Russel Sage Foundation. 1973.

4.    VIEIRA, S. e HOSSNE, W. S. Experimentação com seres humanos. São Paulo: Moderna, 1986.

  

Distribuição de probabilidades

Absorver o conceito de aleatoriedade é muito mais importante do que absorver o conceito de causa e efeito. Mas como você sabe que é o acaso que determina o resultado do jogo de uma moeda, você tem consciência do que é casual ou aleatório.

A variável aleatória quando o acaso tem influência em seus valores.

Função é uma relação matemática que associa cada elemento de um conjunto chamado domínio a um elemento de outro conjunto chamado codomínio (ou contradomínio): 

                                              f:A→B

                       em que:

·  A: é o domínio da função.

·  B: é o codomínio da função.

·  Para cada x ∈ Ax, a função f associa um único y ∈ By. 

EXEMPLO

É dada a função f(X) = 2 X. O domínio da função é o conjunto de inteiros 1; 2; 3. Logo, o codomínio será 2; 4; 6. Veja abaixo.

A variável discreta é contável em determinado período de tempo. Não pode assumir qualquer valor em dado intervalo.

                                                       EXEMPLOS

Número de carros em um estacionamento; número de moedas que você tem no bolso; número de alunos na sala de aula; número de ovos em uma cesta; número de dias úteis na semana; número de chamadas telefônicas em um escritório. 

A variável discreta é contável em determinado período de tempo. Não pode assumir qualquer valor em dado intervalo.                                          

Função de probabilidade é a função de uma variável aleatória discreta que fornece a probabilidade de ocorrer qualquer um dos valores que estão no domínio dessa variável. É indicada por P. A função de probabilidade tem as seguintes propriedades:

1.    A probabilidade de ocorrer qualquer um dos valores possíveis de X é maior do que zero.

                               P (X =x) ≥ 0

 2.    A soma das probabilidades de ocorrência de todos os valores possíveis de X é, obrigatoriamente, igual a 1. 

                             

Distribuição de probabilidades é uma equação ou uma tabela que relaciona cada resultado possível de uma variável aleatória discreta com sua probabilidade de ocorrência.

                                                   EXEMPLO

Seja X o número de caras que podem ocorrer quando se joga uma moeda duas vezes.  Veja o diagrama de árvore e a função de probabilidade  por abaixo. 

                                                                   

A mais simples distribuição de probabilidades é a chamada distribuição uniforme – em que todos os resultados possíveis ocorrem com a mesma probabilidade, isto é,

EXEMPLO

Seja X o resultado que pode ocorrer quando se joga um dado bem balanceado.  A distribuição de probabilidades para x = 1; 2; 3; 4; 5; 6 é 

                                          

É importante saber que variável aleatória não significa variável que pode assumir qualquer valor (um número aleatório). Significa variável que tem um conjunto de resultados possíveis e cada resultado tem determinada probabilidade de acontecer. A palavra “aleatória” indica apenas que os resultados se sucedem ao acaso – sem que você saiba qual resultado irá ocorrer. 

EXEMPLO

Seja X o resultado que pode ocorrer quando se joga um dado bem balanceado.  A distribuição de probabilidades é 

 

         VEJA TAMBÉM:

 Distribuição Normal: Por que é tão comum?

Uma variável aleatória contínua pode assumir qualquer valor dentro de um dado intervalo. Existe, portanto, um número infinito de valores possíveis considerando dois valores. Por exemplo, altura de pessoas é uma variável contínua. Entre dois valores possíveis quaisquer – como 1,70 m e 1,80 m – podem ser encontrados infinitos valores.

A distribuição dos valores possíveis de uma variável contínua é descrita por uma função de densidade de probabilidade (ou simplesmente função de densidade). Vamos começar entendendo o que é distribuição. E – para isso – vamos ver a distribuição normal.

    Distribuição normal

 A distribuição normal, também referida como distribuição de Gauss e curva do sino, é a mais conhecida das distribuições.

Mas... Por que a distribuição normal aparece tanto?

A curva normal já era conhecida há bastante tempo quando Gauss, o grande matemático e astrônomo do século XIX, fazendo medições em seus estudos de astronomia, constatou que:

🔹 Quando são feitas várias medições, o valor mais provável para a resposta real é a média das medições.

🔹 Erros pequenos são mais prováveis do que erros grandes.

🔹Para qualquer número E, ter erro +E é tão provável quanto ter erro -E.

 

A partir dessas suposições simples, Gauss criou a “fórmula” (função de densidade de probabilidade) da distribuição normal e usou essa distribuição para estudar erros de medição.

Vamos olhar primeiro o aspecto gráfico da distribuição. É uma curva em forma de sino, simétrica em torno da média. A probabilidade de a variável aleatória assumir qualquer valor dentro de determinado intervalo é dada pela altura da curva. Isto significa que, se estivermos estudando erros de medição, a probabilidade de erros positivos é igual à probabilidade de erros negativos.

Ainda, erros pequenos (próximos da média) são mais prováveis do que erros grandes (longe da média). Isso dá a configuração da curva, mostrada na figura.

Gráfico da curva normal

Exemplo intuitivo

Para mais bem compreender a questão dos erros, um exemplo excelente é dado por Mlodinov:

Imagine que vamos fazer 150 pães um a um, seguindo uma receita que produz pães com 500 gramas. Por simples acaso, poderemos colocar mais, ou menos, farinha e/ou leite e/ou açúcar em alguns pães. O forno pode estar mais quente, ou menos quente. Pode haver variações de umidade no ar e temperatura ambiente.

O fato é que, no final, teremos alguns pães com mais do que 500 gramas, outros com menos e a maioria com pesos muito próximos de 500 gramas.

O peso de nossos pães irá variar de acordo com a distribuição normal. Por quê? Porque sobre o peso de nossos pães atuou grande número de variáveis aleatórias independentes – algumas atuaram para aumentar o peso, outras para diminuir. Cada variável tem efeito pequeno, mas os efeitos se somam.

Distribuição de pesos dos pães (imagem ilustrativa)

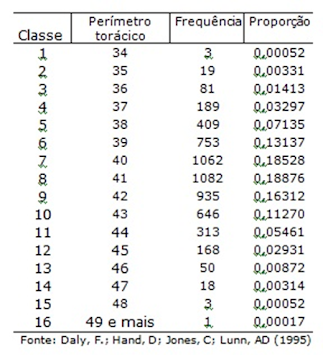
Foi Quetelet, matemático e sociólogo do século XIX, quem achou que poderia aplicar a “lei dos erros” ao ser humano. Fez medições em 5732 soldados escoceses. A tabela abaixo apresenta a distribuição de frequências para o perímetro torácico.

               Distribuição de frequências para o perímetro torácico de homens adultos, em polegadas 

Observe a tabela. Como a variável é contínua, pode ser mostrada por um histograma, como mostrado na figura dada em seguida.

 

Histograma para a distribuição de frequências do perímetro torácico de homens adultos, em polegadas

 A distribuição normal se ajusta ao histograma, como mostra a figura.

 

Gráfico da distribuição normal ajustada ao histograma

Características da distribuição normal    

 

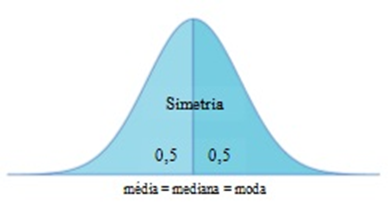
🔹  A área total sob a curva é 1.

🔹  Média, mediana e moda coincidem e estão no centro da curva.

🔹 A curva é simétrica em torno da média: 50% dos valores estão abaixo da média, 50% acima.

 

Gráfico da distribuição normal

A distribuição normal fica definida quando são dados dois parâmetros: a média (representada pela letra grega μ) e o desvio padrão (σ). Mudando esses valores, o aspecto da curva também muda.

Gráfico de três distribuições normais

 

Conclusão

Medidas biológicas, industriais e erros de medição são influenciadas por várias causas aleatórias. Por isso, a distribuição normal aparece com frequência: ela é o resultado natural da soma de pequenos efeitos aleatórios.

Referências

• Mlodinow, L. O andar do bêbado. Rio de Janeiro: Zahar, 2009.

• Daly, F.; Hand, D; Jones, C.; Lunn, A.D. Elements of Statistics. Addison Wesley, 1995.

• https://onlinestatbook.com/2/normal_distribution/intro.html

• https://onlinecourses.science.psu.edu/stat414/node/97

• https://stattrek.com/statistics/dictionary.aspx?definition=Probability-density-function

• https://www.morris.umn.edu/~sungurea/introstat/history/Quetelet.html

 

 

     

           

Um exemplo simples

Leonard Mlodinow explica que, ao assar 150 pães de 500g cada, pequenas variações nos ingredientes, temperatura e umidade fazem com que o peso final varie de forma aleatória. A maioria dos pães terá peso próximo de 500g, mas alguns serão mais leves ou mais pesados.

✅  Conclusão

O resultado é uma distribuição normal, pois muitos fatores aleatórios, atuando independentemente, se somam.

O resultado é uma distribuição normal, pois muitos fatores aleatórios, atuando independentemente, se somam.

                                                       Veja mais em:

1. Mlodinow, L. O andar do bêbado. Rio de Janeiro: Zahar, 2009.

2. Daly, F.; Hand, D; Jones, C.; Lunn, A.D. Elements of Statistics. Addison Wesley, 1995.

3. https://onlinestatbook.com/2/normal_distribution/intro.html

4. https://onlinecourses.science.psu.edu/stat414/node/97

5. https://stattrek.com/statistics/dictionary.aspx?definition=Probability-density-function

6. https://www.morris.umn.edu/~sungurea/introstat/history/Quetelet.html

   

Teste de Tukey: o teste das diferenças honestas

Uma análise de variância (ANOVA) testa a hipótese de igualdade entre as médias populacionais de vários grupos. No entanto, essa análise não identifica quais grupos possuem médias estatisticamente diferentes entre si. O teste F realizado na ANOVA testa a hipótese

                                        H₀: m₁=m₂= … =m_k

contra a hipótese de que existe pelo menos uma diferença de médias diferente de zero. Pelo fato de não identificar onde estão as diferenças, o teste F realizado na ANOVA é conhecido como teste global ou omnibus test.

De qualquer forma, se a análise de variância resulta significante, o pesquisador procura um teste para comparar as médias duas a duas (pairwise comparisons) e assim identificar os grupos que diferem entre si. Neste post, trataremos um desses testes - o teste de Tukey -provavelmente o mais utilizado nessas situações.                              

Na prática, é bastante conveniente o fato de o pesquisador não precisar definir, já no projeto de pesquisa,  quais comparações fará. E isto o teste de Tukey faz: realiza comparações não planejadas (unplanned comparisons). Por essa razão, é considerado um teste a posteriori (post-hoc). 

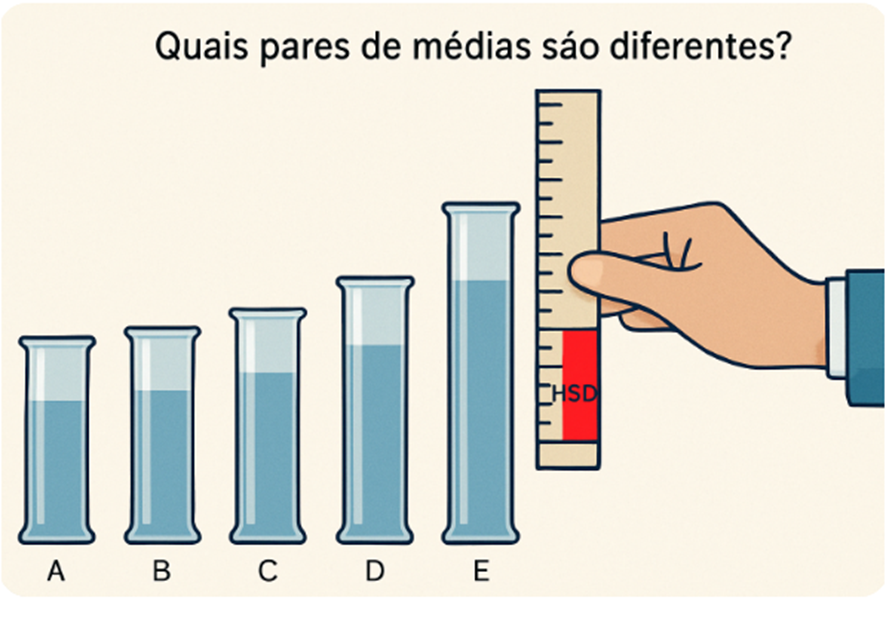
🧩 Procedimento para o teste de Tukey

Para aplicar o teste de Tukey, é preciso calcular a diferença honestamente significante que deve existir entre duas médias para que elas possam ser consideradas significantemente diferentes, a um dado nível  α. 

Essa diferença, indicada por HSD,  é dada pela fórmula:

Onde:

·  q_(k,gl,α) é a amplitude estudentizada, valor que se obtém em tabela e está associado ao número de grupos (k), aos graus de liberdade do resíduo (gl) e ao nível de significância (α);

·  QMR é o quadrado médio do resíduo da ANOVA;

·  r é o número de repetições por grupo.

Duas médias são consideradas estatisticamente diferentes no nível de significância estabelecido (α) sempre que o valor absoluto da diferença entre elas for maior ou igual à HSD.

                🛑  Como usar a tabela de amplitude estudentizada q

Veja o trecho da tabela apresentado a seguir. O valor em negrito corresponde à comparação de médias em um experimento com seis tratamentos (k=6) e 24 graus de liberdade no Resíduo da ANOVA (gl=24), com nível de significância de 5%.

Tabela

Valores de q para α=5%

💡 Observe: Nos softwares e na literatura em inglês, é comum usar a sigla HSD (Honestly Significant Difference)  para identificar a diferença honestamente significante calculada no teste de Tukey. No Brasil, essa diferença costuma ser chamada de diferença mínima significante e é  representada pela letra grega Δ(delta).

Contudo, vale uma observação importante: em língua inglesa, o termo Least Significant Difference (LSD) refere-se especificamente ao teste de Fisher. No caso do teste de Tukey, a diferença mínima entre médias é chamada de Honestly Significant Difference (HSD),  denominação dada por seu autor, John W. Tukey.

                                         🔍 EXEMPLO

Considere os dados de diminuição da pressão arterial, apresentados na Tabela 1. Esses dados foram submetidos a uma análise de variância (Tabela 2). Como o valor de F é significante no nível de 5%, concluímos que existe pelo menos uma média diferente das demais. As médias dos grupos são apresentadas na Tabela 2.

Tabela 1

Diminuição da pressão arterial (mmHg) segundo o grupo

 

Tabela 2

Médias da diminuição da pressão arterial por grupo

Tabela 3

Análise de variância (ANOVA)

Queremos saber quais médias são significativamente diferentes entre si. Para isso, vamos aplicar o teste de Tukey.

Cálculo da HSD

·     q = 4,3727: valor da tabela de q para k=6, gl=24, α=5%;

·     QMR =36,00: quadrado médio do resíduo da ANOVA;

·     r = 5: número de repetições por grupo.

Comparações de Médias

Agora, comparamos as médias duas a duas. As diferenças significantes no nível de 5% estão indicadas com um asterisco.

Tabela 4

Diferenças de médias da diminuição da pressão arterial

 

✅ Conclusão De acordo com o teste de Tukey, no nível de 5% de significância:

              ·  a média do tratamento A é maior do que a de B e a do controle;

              · a média do tratamento D é maior do que as médias de B, C, E e controle. 

                                          🧩 Outputs

1. MINITAB

Tukey Pairwise Comparisons 

 Grouping Information Using the Tukey Method and 95% Confidence

 

  Treatment   N   Mean  Grouping

  D                5   29,00     A

  A                5   21,00     A  B

  E                5   13,00         B  C

  C                5   10,00         B  C

  B                5     8,00              C

  Control       5     2,00              C

 Means that do not share a letter are significantly different.

2. SAS

 

                          Error Mean Square              36

              Critical Value of Studentized Range  4.37265

                   Minimum Significant Difference    11.733

 

 Means with the same letter are not significantly different.

 

                      Tukey Grouping          Mean      N    trat

 

                                      A                29.000        5     4

                                      A 

                              B      A               21.000         5     1

                              B

                              B      C               13.000         5    5

                              B      C

                              B      C               10.000         5    3

                                      C

                                     C                 8.000        5    2        

                                     C                 2.000        5    6

              ·  a média do tratamento A é maior do que a de B e a do controle;

              · a média do tratamento D é maior do que as médias de B, C, E e controle. 

                                          🧩 NOTA

Entenda  resultados  indicados por letras, usuais em outputs de softwares: 

· quando letras diferentes aparecem em frente a duas médias, a diferença entre essas médias é estatisticamente significante; 

· quando a mesma letra aparece em frente a duas médias, a diferença entre essas médias não é estatisticamente significante.

Tabela 5

  Comparação das médias de diminuição da pressão arterial