Hypothesis Tests on a Single Standard Deviation

                       

                     📌  Chi-square distribution

If Z is a random variable with a standardized normal distribution (mean zero and variance 1), then Z² has a chi-square distribution with 1 degree of freedom. 

 Z ∩ N (0,1)  Þ Z² ∩ c² (1df)

If Z₁, Z₂, ……, Z_k, are a set of independent and identically distributed standard normal variables, then the sum of their squares has a chi-square distribution with k degrees of freedom. 

                                                

Let X_i be k independent and normally distributed random variables with mean µ and variance σ²

 1. Then (X_i - µ), i from 1 to k, has mean zero and Σ (X_i - µ)² has a chi-square distribution with k degrees of freedom.

                               

                                                   🤯   EXAMPLE

In a city where police officers rely on speed radars that require regular calibration, a specialized center ensures that these devices operate correctly. Experts at the center have established that, in an urban area, radar speed readings (X_i) follow a normal distribution with a mean of 25 mph and a standard deviation of 3 mph:

·     Mean: μ = 25 mph

·     Standard deviation: σ = 3 mph

The manager of the center is considering purchasing new radars and has received proposals from two manufacturers. Both manufacturers claim that their radars produce speed readings that are normally distributed with a mean of 25 mph and a standard deviation of 1 mph.

🛑 Testing the First Manufacturer

To test the first manufacturer's claim, the manager instructs a technician to take five speed measurements using a test car programmed to travel exactly at 25 mph. The recorded speeds are:

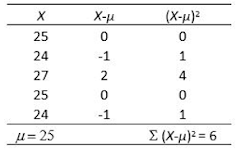
                                                    25, 24, 27, 25, 24

At a significance level of α = 10%, the null hypothesis is H₀: σ = 1 (the radar's standard deviation is 1 mph, as claimed.).

To test this claim, we calculate the variance:

                                                                              

The sum of squared deviations from the mean, ∑ (Xi − μ)² = 6. For a significance test at α = 10% with 5 degrees of freedom, the chi-square critical values are obtained. The calculated chi-square value of 6 falls within the acceptance region.

Conclusion: Since the calculated chi-square value of 6 falls within the acceptance region, the null hypothesis cannot be rejected. Then, the claim that the radar has a standard deviation of 1 mph is accepted. The first manufacturer's radar appears to be properly calibrated in terms of variance.

                                          🛑  Testing the Second Manufacturer

A second radar is tested under identical conditions. The recorded speeds are:

                                                              28, 27, 30, 28 ,29

If the radar readings are assumed to be normally distributed with a mean of 25 mph, we test the claim H₀: σ = 1.

Let's calculate the variance of X :

The upper critical chi-square value for α = 10% and 5 degrees of freedom is 11.07. Since the calculated sum of squared deviations (63) exceeds the upper critical value, it falls in the rejection region.

The  null hypothesis is rejected at the 10% significance level, indicating that the assumed variance does not hold. The second radar does not meet the claimed standard deviation of 1 mph, suggesting it is unreliable.

                        🛑 Reevaluating the Second Radar Using Sample Mean

While the variance test suggests the radar is unreliable, another issue is whether the radar is correctly measuring 25 mph. Instead of using the assumed mean (μ = 25 mph), we calculate the sample mean:

Conducting a hypothesis test for mean:

Using the known standard deviation (σ = 1 mph) and sample size (n =5), we can conduct a hypothesis test for the mean , applying the z-test :

where

Then, we have:

The critical z-value at α = 10%  is 1.645.

Since 7.60 is far beyond the critical z-value, we reject H₀. This confirms that the second radar is not correctly calibrated, as its mean is significantly different from 25 mph.

However, we could also calculate the sample variance, instead of using the assumed variance ((σ = 1 mph), and apply the t-test:

Let's calculate the variance of X :

The critical t-value at α = 10% and 4 degrees of freedom is 1.533.

Since 6.67 is far beyond the critical z-value, we reject H₀. This confirms that the second radar is not correctly calibrated, as its mean is significantly different from 25 mph.

                                                     ✅ Final Decision

·     The first manufacturer's radar passes the variance test and seems to be properly calibrated.

·     The second manufacturer's radar fails both the variance and mean tests, indicating a significant calibration error.

Recommendation: The center should accept the first manufacturer's radar and reject the second one due to its inaccuracy in measuring speed correctly.