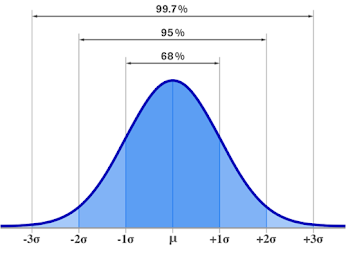
A representação
gráfica da distribuição normal é uma curva em formato de sino, simétrica em torno da média. Portanto, metade dos valores da
variável aleatória X são
iguais ou superiores à média e a outra metade são iguais ou inferiores à média. A curva abriga 100% da
população, ou seja, todos os possíveis valores
que que a variável aleatória pode assumir estão sob a curva. A distribuição normal é definida
por dois parâmetros: a média, representada por µ e o desvio padrão, representada
por σ.
1. O limite
de velocidade em uma determinada estrada é de 40
km/h, com tolerância de 7 km/h. A velocidade de um
motorista que viaja nesta estrada é uma variável aleatória
com média μ = 40 km/h e desvio padrão σ = 4 km/h. Qual é a
probabilidade de esse motorista ultrapassar 47 km/h e ser multado?
Vamos
padronizar a variável, que terá então média zero e desvio padrão 1 e procurar a
probabilidade associada a essa variável em uma tabela de distribuição normal padronizada
ou reduzida, encontrada no apêndice da maioria dos livros didáticos de estatística.
Calcule:
RESPOSTA:
A probabilidade pedida é 4%.
NOTA:
Você pode achar a probabilidade usando software.
2. Em condições normais de operação, a média das medidas feitas por um radar é µ = 25 mph e o desvio padrão é σ = 3 mph. Um carro de teste com velocidade fixada em 25 mph é normalmente utilizado para verificar se o radar está calibrado. Considerando que o radar está em boas condições, isto é, que µ = 25 mph e σ = 3 mph, qual é a probabilidade de o radar atribuir ao carro de teste velocidade: a) 28 mph ou mais? b) 27½ mph ou mais? c) Qual é a velocidade limite para que a probabilidade de serem medidas velocidades maiores que ela seja 5%?
a) Probabilidade de medir 28 mph ou mais
b) Probabilidade de medir 27½
mph ou mais
RESPOSTA: A probabilidade pedida é de 0,20327,
aproximadamente 20%.
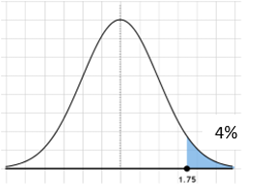
c) Velocidade que delimita 5% de probabilidade de medir
as velocidades maiores
LEMBRE-SE
DE QUE
Mais
controle significa erros menores. É preciso ter isso em mente quando se quer
mais qualidade. Compare as probabilidades obtidas nos exemplos 2b, 3 e 4.
EXERCÍCIOS
3. Revise o problema anterior. Para testar se 4 radares que operam conjuntamente estão calibrados, é utilizado
um carro de teste com velocidade fixada em 25 mph. Quando calibrados, as medições feitas por cada radar
é uma variável aleatória independente com distribuição normal de média µ =25 mph e desvio
padrão σ = 3 mph. Se os radares estiverem em condições normais de trabalho, qual é a probabilidade de a média das medições feitas por eles ser igual ou maior que 27½ mph?
4. A ideia de usar 4 radares é
boa, mas usar 9 radares é melhor. Para verificar se 9 radares que operam conjuntamente estão calibrados, é utilizado um carro de teste com velocidade fixada em 25 mph. A velocidade de cada radar, quando calibrado, é uma variável aleatória com
distribuição normal de média µ =25 mph e desvio padrão σ = 3 mph. Qual é a
probabilidade de a média das medições feitas pelos 9 radares ser igual ou superior a 27½ mph?
OPERAÇÕES COM VARIÁVEIS ALEATÓRIAS
EXERCÍCIO
5. Supondo que o horário de chegada do metrô seja uma variável aleatória com média µ1 = 8h10min e desvio padrão σ1 = 40s, e que a sua chegada na estação seja uma variável aleatória com média µ2 = 8h08min e desvio padrão σ2 =30s, qual é a probabilidade de você não conseguir pegar o metrô?
Faça M indicar o horário de
chegada do metrô e V indicar seu horário de chegada na estação. Então, W = M - V,
seu tempo de espera, é uma variável aleatória com distribuição
normal de média 8:10 – 8:08 = 2 min = 120 s, variância 402 + 302
=1600 + 900 = 2500 s e desvio padrão 50.
Você não consegue pegar o trem se W ≤ 0. Para achar a probabilidade de W ≤ 0:
REGRA DE DECISÃO
Imponha valores críticos para
rejeitar determinados resultados. Em controle da qualidade, isso é essencial.
EXERCÍCIOS
6. Em uma indústria de alimentos enlatados, o nível de acidez (pH) do
produto em cada lata é uma variável aleatória com distribuição normal de média
7 e desvio padrão 0,5. A lata é rejeitada toda vez que o produto apresentar pH inferior a 6,0 ou superior a 8,0. Qual é a probabilidade de isso
acontecer?
7. O fabricante de determinado produto alimentício
vendido em pacotes de 3kg quer saber se o peso médio de seu
produto varia significativamente de 3 kg. Se, no nível
de significância de 1%, o peso médio diferir significativamente de 3
kg, o fabricante ajusta a balança. A experiência mostra que o desvio
padrão é 0,03kg. O peso médio de uma amostra aleatória de novas embalagens foi de
2,991 kg. O resultado ajuda decidir se o peso médio do
pacote é significativamente diferente de 3kg?
RESPOSTA: O peso médio do pacote não difere de 3 kg, significativamente.
No comments:
Post a Comment