
Análise de Dados Categóricos em Tabelas 2 x 2
Considere os dados apresentados
na Tabela 1, que representa uma tabela 2 x 2 com dados categóricos.
Temos dois grupos distintos de unidades (por exemplo, pessoas, animais ou
objetos), que chamaremos de Grupo A e Grupo B. Em cada grupo, observamos dois
tipos de eventos: "sucesso" e "fracasso".
Tabela 1
Distribuição de sucessos e fracassos segundo o
grupo
Observe agora o exemplo numérico apresentado na Tabela 1 e na Figura 2, só para tornar
a situação mais concreta.
Tabela 2
Sucessos e fracassos por grupo
Figura 1
Sucessos e fracassos por grupo
Para analisar esses dados,
podemos adotar duas abordagens principais, conforme discutido a seguir.
1.
Perspectiva Binomial
Nesta abordagem, assumimos que
cada grupo tem sua própria probabilidade de sucesso — denotadas por θ1
e θ2. Considera-se que os eventos são
independentes dentro de cada grupo. Isso nos leva a modelar os números de
sucessos como variáveis aleatórias com distribuições binomiais distintas para cada grupo.
Para testar a hipótese de que as
probabilidades são iguais, isto é:
H0:θ1=θ2,
podemos aplicar o teste qui-quadrado
de independência, desde que o tamanho da amostra seja suficientemente
grande (regra prática: n ≥ 40), o que assegura uma boa
aproximação pela distribuição qui-quadrado.
2.
Perspectiva Hipergeométrica
Outra forma de ver o problema surge quando o número total de sucessos está fixado. Neste caso, o que fazemos é redistribuir esses sucessos entre os dois grupos — ou seja, observamos a variabilidade condicional à soma total de sucessos. Esse é o cenário ideal para aplicar a distribuição hipergeométrica. Essa é a base do chamado teste exato de Fisher, que é apropriado quando:
· O tamanho da amostra é pequeno (n < 40);
· Os totais marginais são fixos por desenho
experimental;
· Há frequências esperadas menores do que 5 em
uma ou mais células (condição que viola os pressupostos do teste qui-quadrado).
Procedimento
para o Teste Exato de Fisher
Quando se aplica o teste exato
de Fisher, costuma-se apresentar uma tabela como a Tabela 3, seguida de uma
fórmula que calcula a probabilidade exata de ocorrência daquela configuração:
Tabela 3
Representação tabular de uma tabela 2 x 2
Embora o cálculo da probabilidade exata envolva fatoriais (notação "!"), o que pode ser demorado manualmente, hoje esse teste é feito exclusivamente por computador.
Para tornar mais concreto, considere o seguinte exemplo.
Tabela 4
Distribuição dos participantes segundo grupo e
sobrevivência
(distribuição hipergeométrica com N1=3, N2=3, n=3)
Neste caso, nenhum estatístico
aplicaria um teste qui-quadrado, pois a aproximação pela distribuição normal é
inadequada. De qualquer modo, este exemplo é importante porque foi este o
exemplo original utilizado por Fisher para ilustrar o teste que leva seu nome.
Ainda, o exemplo é didático, pois uma das células contém valor zero, o que sugere uma associação extrema — todos os participantes de um grupo responderam da mesma forma. Veja a Figura 2.
Figura 2
Quando
isso não ocorre (isto é, todas as células têm valores positivos), é
necessário calcular também a probabilidade de ocorrerem desvios ainda mais
extremos, sob a hipótese nula. Veja um exemplo com menor associação. O p-valor,
pelo teste de Fisher (1), é p-valor = 0,04545<0,05.
Tabela 5
Distribuição dos participantes segundo o fato de terem ou não sido vacinados e terem ou não tido gripe.
Afinal, qual
é o teste?
Se considerarmos duas
distribuições binomiais, podemos calcular a probabilidade de observar, por
exemplo, x1 sucessos no Grupo A e x2 no Grupo B. Aplicamos então o teste de qui-quadrado.
Se o número total de
sucessos estiver fixado, ou seja, tivermos x = x1+x2, então a distribuição condicional dos sucessos entre
os grupos é hipergeométrica. Neste caso, devemos aplicar o teste exato de Fisher.
Implicações
da Abordagem Hipergeométrica
Quando aplicamos o teste exato
de Fisher, estamos implicitamente:
· Fixando os totais marginais da tabela 2 x 2;
· Fixando o número de sucessos no Grupo A (e, por consequência, todas as outras
células, dado que só há um grau de liberdade);
· Não mais testando diretamente a igualdade dos
parâmetros θ1 e θ2, como na
abordagem binomial.
Nesse contexto, o parâmetro
comum θ (sob H0) passa a ser um parâmetro de
distúrbio (nuisance parameter). Ou seja, não estamos interessados no
seu valor exato, mas apenas em saber se número de sucessos é estatisticamente o
mesmo nos dois grupos.
Nota: Para aprofundar o entendimento sobre a distribuição hipergeométrica, consulte as três postagens sobre Distribuição Hipergeométrica deste blog. Para explicações sobre o teste exato de Fisher, consulte o Capítulo 3 do livro Bioestatística: tópicos avançados, visto abaixo.
EXERCÍCIOS
📘 Exercício 1: Veja a tabela 2 x 2:
1. Calcule as proporções de sobrevivência nos dois
grupos.
2. Qual seria sua hipótese de nulidade para o teste
qui-quadrado?
3. A frequência esperada em cada célula é maior do que 5?
4. Qual teste você aplicaria nesse caso: qui-quadrado
ou Fisher?
📘 Exercício 2: Aplicando o teste exato de Fisher
Veja a tabela:
1. Por que o teste qui-quadrado não é adequado neste caso?
2. Use uma calculadora online ou software para aplicar o teste exato de Fisher.
3. Interprete o p-valor obtido: há evidência de
associação entre grupo e sucesso?
📘 Exercício 3: Distribuição hipergeométrica
Em um experimento, há 6 bolas: 3
vermelhas e 3 azuis. Três são sorteadas ao acaso.
1. Qual a probabilidade de obter exatamente 2
vermelhas no sorteio?
2. Identifique os parâmetros da distribuição
hipergeométrica.
3. Relacione esse exemplo com o contexto de tabelas 2
x 2 fixando totais marginais.
RESPOSTAS
1.
Proporções de sobrevivência
· Tratamento
A: 8/10 = 0,80
· Tratamento
B: 4/10 = 0,40
H1: Há associação entre tratamento e sobrevivência.
3.
Frequência esperada em cada célula
Exemplo: Para tratamento A e Sim
As outras
esperadas são:
· A/Não: 4
· B/Sim: 6
· B/Não: 4
📘 Exercício 2: Aplicando o teste exato de Fisher
2. Teste
exato de Fisher
Use um software. O p-valor é
aproximadamente 0,2429, não significante.
✅ Exercício 3: Pensando em distribuição
hipergeométrica
1.
Probabilidade de obter exatamente 2 vermelhas no sorteio
· População
total N=6
· Sucessos na
população K=3 (vermelhas)
· Tamanho da
amostra n=3
· Procuramos P(X=2),
isto é, 2 vermelhas em 3 sorteios.
A fórmula
da hipergeométrica:
Substituindo:
2.
Parâmetros:
· N=6, K=3, n=3,
k=2
3. Relação
com tabelas 2 x 2
Suponha que vermelha = "sucesso" e azul = "fracasso". São dois grupos (A e B), cada um com 3 bolas. Sortear 3 bolas seria como fixar o total de sucessos (vermelhas) e redistribuí-los entre dois grupos, como se fossem duas linhas da tabela. Esse é exatamente o espírito do teste de Fisher: condicionar os totais marginais e modelar a redistribuição dos sucessos.










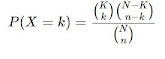

2 comments:
Suas postagens são ótimas, estou seguindo seu blog e curtindo bastante!! Parabéns!
Meu Blog: Letícia Alves
Obrigada, vou já ver seu blog.
Post a Comment