Para entender a questão do p-valor, é preciso um pouco de
história da Estatística. Existem duas escolas de pensamento sobre testes de
significância. O primeiro foi popularizado por Ronald A. Fisher na década de
1920. Fisher via o p-valor não como uma parte de
um procedimento formal para testar hipóteses, mas como um método informal de
ver quão surpreendente pode ser um conjunto de dados. O p-valor,
quando combinado com a experiência do pesquisador e seu conhecimento do
assunto, pode ser útil para interpretar novos dados.
Depois que o trabalho de Fisher foi apresentado, Jerzy Neyman e Egon
Pearson abordaram a questão de outra forma. É preciso lembrar que, em ciência,
é importante limitar dois tipos de erros: falsos positivos, quando
você acha que é real algo que não existe, e falsos negativos,
quando você acha que algo que ocorre não é real.
Apenas como exemplo, considere um teste laboratorial para o diagnóstico
de determinada doença. O teste pode apresentar dois tipos de erros: falso
positivo, quando diz que o paciente é doente, mas não é; e falso
negativo, quando diz que o paciente não é doente, mas é. Em Estatística, é
convenção chamar o falso positivo de erro Tipo I e o falso
negativo de erro tipo II.
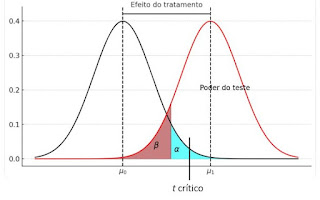
📌 Erro Tipo I (falso positivo): quando
você diz que um tratamento tem efeito (afirma) e esse tratamento não tem
efeito.
📌Erro Tipo II (falso negativo): quando você
diz um tratamento não tem efeito (nega) e esse tratamento tem
efeito.
Falsos positivos e falsos negativos são erros, mas é totalmente
impossível eliminá-los. Se você se precipitar querendo achar efeitos de
tratamentos, estará propenso a obter mais falsos positivos (ou seja, mais erro
Tipo I); se você for conservador, isto é, não se apressar em apontar efeitos de
tratamentos, estará propenso a obter mais falsos negativos (ou seja, mais erro
Tipo II).
Neyman e Pearson raciocinaram que, embora seja impossível eliminar
totalmente os falsos positivos e falsos negativos, é possível desenvolver um
processo de tomada de decisão que garanta que falsos positivos ocorrerão com
probabilidade predefinida. Eles chamaram essa probabilidade de a (nível
de significância) e sua ideia era que os pesquisadores definissem a com
base em suas experiências e expectativas. Por exemplo, quem estiver disposto a
tolerar uma probabilidade de 10% de falsos positivos, define a =
0,1. Mas se precisar ser mais conservador, pode definir a em
0,01 ou menos.
Como isso funciona na prática? No sistema de Neyman-Pearson, definem-se
duas hipóteses: a hipótese de nulidade, isto é, uma hipótese de que
determinado tratamento não tem efeito - bem como uma hipótese
alternativa, de que o tratamento tem efeito. Escreve-se:
📌 H0: efeito do tratamento igual a zero
📌 H1: efeito do tratamento diferente de zero
Em seguida, é feito um teste estatístico para determinar a probabilidade
de obter resultado igual ou maior do que o conseguido quando a hipótese da
nulidade é verdadeira. Esse é o p-valor e o procedimento de
Neyman-Pearson consiste em rejeitar a hipótese da nulidade sempre que p-valor < a.
Ao contrário do procedimento de Fisher, este método não usa,
deliberadamente, a força da evidência obtida em um experimento em particular;
decide, simplesmente, rejeitar ou não a hipótese da nulidade. O tamanho
do p-valor não é usado para comparar experimentos, nem para
tirar conclusões além de "A hipótese da nulidade deve (ou não) ser
rejeitada.”.
Embora a abordagem de Neyman e Pearson seja conceitualmente diferente da
de Fisher, os pesquisadores fundem as duas. A abordagem de Neyman e Pearson é
onde obtemos "significância estatística", com um valor a pré-escolhido,
que garante as probabilidades de falsos positivos no longo prazo. Mas suponha
que você conduza um experimento e obtenha p-valor = 0,032. Se o seu
limite for o convencional a = 0,05, você obteve um resultado
estatisticamente significante. É tentador – embora esteja errado - dizer
"A probabilidade de erro Tipo I é de 3,2%". Isso não faz sentido,
porque um único experimento não determina uma probabilidade de erro Tipo I.
Compare seu experimento com outros, vendo apenas o valor de a.
Quando se diminui um tipo de erro, aumenta-se o outro, considerando o
mesmo problema, sendo resolvido pelo mesmo teste de significância. Mas há
testes com mais poder do que outros. Denomina-se poder do teste a
probabilidade de rejeitar a hipótese da nulidade quando ela é falsa. Então o
melhor teste é aquele que tem a menor probabilidade de falsos negativos para
uma determinada escolha de a.
🔔 NOTA: Esta postagem foi escrita com base em:
REINHART, A. Statistics doing wrong. San Francisco, No Starch Press. 2015.