Medidas repetidas
O termo "medidas repetidas" é usado para
indicar que as mesmas unidades são submetidas a todas as intervenções (os tratamentos)
em um mesmo ensaio. Em outras palavras, um ensaio com medidas repetidas é
aquele em que a mesma unidade é medida tantas vezes quantas forem as
intervenções (ou tratamentos) em teste.
Exemplo
Em um estudo sobre o efeito de uma droga analgésica
em seis participantes, podem ser feitas três medições do alívio da dor com três
drogas diferentes (os tratamentos): uma com a droga A, outra com a droga B e
outra com a droga C. A variável dependente é o alívio da dor.
Exemplo
Um experimento com quatro degustadores (1, 2, 3, 4)
que testam quatro tipos diferentes de café (os tratamentos) é de medidas
repetidas porque um mesmo degustador fornece uma classificação para cada tipo
de café. A variável dependente é classificação do café.
Exemplo
Um pesquisador quer testar o efeito de três
horários (os tratamentos) no tempo de corrida de quatro atletas. O tempo de
corrida, medido em cada horário, é a variável dependente.
Como em todo experimento, as variáveis que
podem ter efeito sobre a variável dependente devem ser, obrigatoriamente,
controladas. No último exemplo, os tratamentos devem ser testados em idênticas
condições de temperatura, insolação, hora e tipo de alimentação servido durante
todo o dia etc.
Importante destacar que, quando falamos em
unidades, não nos referimos apenas a pessoas. Experimentos com medidas
repetidas podem ser conduzidos com plantas, animais, empresas ou objetos.
Pressuposições para a análise de variância (ANOVA)
com
medidas repetidas
As pressuposições para a ANOVA com medidas
repetidas (nas mesmas unidades) são as seguintes:
1. Normalidade da variável dependente
A variável dependente deve seguir uma distribuição
aproximadamente normal para cada nível da variável independente. Essa
suposição é mais importante no caso de pequenas amostras. A ANOVA é
robusta contra violações de normalidade em amostras grandes (Teorema do Limite Central).
2. Ausência de valores discrepantes (outliers)
Valores discrepantes podem distorcer os resultados
da ANOVA. Devem ser identificados e tratados antes da análise.
3. Esfericidade
Se a esfericidade for violada, o teste F da
ANOVA pode ser inflacionado, aumentando o erro tipo I, ou seja, aumentando a probabilidade
de detectar uma diferença estatisticamente significativa quando, na realidade,
ela não existe. Pode ser usado o teste de esfericidade de Mauchly para
avaliar essa pressuposição.
4. 4. Independência
dentro dos sujeitos
As medições dentro de cada unidade experimental
são dependentes (porque são medidas repetidas), mas as medições entre
diferentes unidades devem ser independentes.
O que é
esfericidade?
Definição: Esfericidade é pressuposição fundamental que deve ser satisfeita para justificar uma análise de variância (ANOVA) padrão com dados de experimentos com medidas repetidas.
A esfericidade ocorre quando as variâncias das
diferenças entre todas as combinações possíveis de pares de intervenções (tratamentos
ou grupos) são estatisticamente iguais.
Justificativa: Para realizar uma análise de variância (ANOVA), é
necessário garantir a homogeneidade das variâncias das intervenções (tratamentos
ou grupos). O teste de Levene (2) é um método usado para verificar essa
homogeneidade, quando o experimento é inteiramente ao acaso. Se as variâncias são
homogêneas (homocedasticia), pode ser feita uma análise de variância
unifatorial.
Em análises de experimentos com medidas repetidas na
mesma unidade experimental (pessoa, animal, planta, objeto, empresa), é preciso
testar a esfericidade, pois sua violação aumenta a probabilidade de erro tipo
I, ou seja, aumenta a probabilidade de detectar uma diferença estatisticamente
significante quando, na realidade, ela não existe. Se as variâncias são
homogêneas (homocedasticia), pode ser feita uma análise de variância com dois
fatores, isto é, tratamentos e unidades. A análise de variância com dois
fatores também é conhecida como análise de experimentos em blocos (cada
unidade, seja pessoa, animal, planta, objeto ou empresa) constitui um bloco.
Teste de
Esfericidade de Mauchly
O teste de Mauchly é um procedimento
estatístico usado para verificar a hipótese de esfericidade. No entanto, pode
falhar em detectar desvios da esfericidade quando a amostra é muito pequena
ou muito grande. Mesmo assim, é amplamente utilizado. Se a hipótese de
esfericidade for atendida, a estatística F da ANOVA será válida. Caso
contrário, a estatística F terá viés e a probabilidade de erro tipo I será
aumentada.
Quando as variâncias são muito diferentes (por exemplo, 13,9 vs. 17,4 vs. 3,1), é possível que tenha ocorrido uma violação da esfericidade. Para confirmar, é preciso aplicar o teste de esfericidade de Mauchly. Se o teste indicar um resultado estatisticamente significante, rejeita-se a hipótese de esfericidade, ou seja, a conclusão é a de que as variâncias das diferenças entre os grupos não são estatisticamente iguais. Para corrigir esse problema, podem ser aplicadas algumas correções, como as de Greenhouse-Geisser ou Huynh-Feldt.
Tabela 1
Tempo de corrida, em minutos, de cinco
atletas
segundo o tipo de treinamento

1.
Estabelecer as hipóteses:
· H₀: A matriz de covariância segue a
propriedade de esfericidade (as variâncias das diferenças são estatisticamente iguais.
· H₁: As variâncias são significativamente
diferentes.
2.
Cálculo
da estatística do teste: a estatística de teste é dada por:
onde:
· S é a matriz de covariâncias das diferenças entre
intervenções (tratamentos),
· g é o número de graus de liberdade de tratamentos
(neste caso, 3−1=2),
· det (S) é o determinante da matriz de covariância.
3.
Conversão
para o teste de qui-quadrado: o valor W é
transformado em uma estatística qui-quadrado usando a seguinte fórmula:
onde N é o número de participantes.
4.
Comparação
com a distribuição qui-quadrado: Se o p-valor for menor que 0,05, rejeitamos H0
nesse nível de significância.
Cálculo da esfericidade para os dados da Tabela 1
1. Calcule as diferenças entre cada par de tipo de treinamento dos dados apresentados na Tabela 1. Essas diferenças estão apresentadas na Tabela 2. Calcule as médias e variâncias dessas diferenças.
Tabela 2
Diferenças entre pares de tratamentos
Para garantir que a pressuposição de esfericidade é
atendida, é preciso que as variâncias das diferenças entre os pares de tratamentos
sejam estatisticamente iguais.
Temos
as variâncias das diferenças entre tratamentos na Tabela 2. Precisamos obter as
covariâncias:
A
covariância entre as variáveis e não é simplesmente o produto
das diferenças, como (B-
· Calcule a média de cada variável (), (C-A), (B-C).
·
Subtraia a
média de cada valor individual das varáveis. Por exemplo, X= (B-A) e Y=
C-A), para cada Xi, calcule
Para cada Yi, calcule
· Multiplique essas diferenças ponto a ponto para cada participante:
· Some esses produtos.
·
Divida por
n-1.
Veja o resultado desses cálculos nas Tabelas 3, 4 e
5.
Tabela 3
Cálculos para obter as covariâncias de (B-A) (C-A)
Nota: (B-A)bar significa média da variável (B-A). A mesma notação aparece nas demais tabelas.
Tabela 4
Cálculos para obter as covariâncias de (B-A) (C-B)
Tabela 5
Cálculos para obter as covariâncias de (C-A) (C-B)
Das Tabelas 3, 4 e 5 podemos obter:
Cov(C-A)(C-B)=0,0730/9=0,008111
A matriz de covariâncias, que chamaremos de S, está apresentada na Tabela 6.
Matriz S de covariâncias
Agora que você tem a matriz S, calcule a
estatística de Mauchly:
O determinante de S (3) é −1,165×10−22
(um valor muito pequeno, próximo de zero).
O traço da matriz é dada pela soma dos elementos da diagonal principal:
Conclusão
O teste de esfericidade de
Mauchly foi conduzido para avaliar se a pressuposição de esfericidade foi
satisfeita. No entanto, o determinante da matriz de covariância foi próximo de
zero, resultando em um valor negativo para a estatística .
Isso impossibilitou o cálculo da estatística qui-quadrado. Esse resultado
sugere uma violação severa da esfericidade,
tornando a suposição inadequada para a ANOVA de medidas repetidas.
Dado esse cenário,
recomenda-se o uso de correções para
esfericidade, como o ajuste Greenhouse-Geisser
ou Huynh-Feldt, ou ainda considerar
abordagens alternativas, como modelos de efeitos
mistos, que não exigem a suposição de esfericidade.
Justificativa para o resultado:
1.
As
variâncias das diferenças entre condições são muito diferentes:
o Var(B−A) = 0,00711
o Var (C−A) = 0,01111
o Var(C−B )= 0,02711
Se a
esfericidade fosse atendida, essas variâncias deveriam ser aproximadamente
iguais.
2. O determinante da matriz de covariância é muito próximo de zero (−1.165×10−22), o que indica multicolinearidade extrema e forte violação da esfericidade.
3. O teste de Mauchly não pôde ser concluído porque W ficou negativo, impossibilitando o cálculo de χ2.
4. A vantagem de o exemplo não ter chegado à
estatística de Mauchly é deixar claro que isso acontece. Rejeite H0.
Veja:
1.Field, A. Descobrindo a Estatística usando o SPSS.2 ed. Porto Alegre:
Artmed,2009.
2.Sphericity. Disponível em: https://statistics.laerd.com/statistical-guides/sphericity
-statistical-guide.php. Acesso em
24 de março de 2020.
3.Frost, J. Repeated measures designs: benefits and an ANOVA
Example. Disponível
em: https://statisticsbyjim.com/anova/repeated-measures-designs-benefits-anova-example/Acesso em
23 de março de 2020.
4. Zaiontz, C. Sphericity: Basic concepts. https://real-statistics.com/anova-repeated-measures/sphericity/



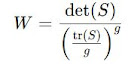







No comments:
Post a Comment