p-valor pequeno traz validade ao trabalho?

A grande maioria dos trabalhos em ciência experimental tem como objetivo testar o efeito de uma intervenção ou das diferenças entre os efeitos de diversas intervenções. Por exemplo, diante da pergunta: ”Esta nova droga tem efeito?”, quer você busque a resposta na literatura, quer conduza um experimento, a estatística certamente entrará na história. E como a estatística entra na história? Os estatísticos calculam a diferença estatisticamente significante que permite ao pesquisador tomar decisão em condições de incerteza. Vamos discutir isso.

Imagine que você quer testar uma nova droga para diminuir a duração de um resfriado. Para fazer isso, acha 100 pacientes com resfriado e, para 50 deles tomados ao acaso, fornece a nova droga (grupo tratado). Aos outros 50 fornece um placebo (grupo controle). Os pacientes serão examinados duas vezes ao dia para registrar o tempo de duração dos resfriados de cada um. Mas resfriados não têm a mesma duração: algumas pessoas têm resfriados com duração mais longa, outros com duração mais curta. É a variabilidade, que o estatísticos medem calculando o desvio padrão. De qualquer forma, imagine que, terminado o experimento você verifica que nos 50 pacientes do grupo tratado os resfriados perduram em média dois dias a menos que nos pacientes do grupo controle. Você pode dizer que a nova droga realmente funciona?

A resposta é dada por um teste de hipóteses, também conhecido como teste de significância. Aplicando o teste, você terá resposta para a pergunta: “Se a nova droga não tem efeito, qual é a probabilidade de o experimento ter chegado a um resultado igual, ou mais extremo do que o obtido?” É possível calcular essa probabilidade. Para isso, é preciso formalizar a hipótese da nulidade (H₀), que pode ser escrita como segue:

                    H₀: a nova droga não tem efeito.

Considerando verdadeira a hipótese da nulidade, calcula-se a probabilidade de serem obtidos resultados iguais, ou mais extremos dos que o que foram obtidos. É o que se chama p-valor. Pense bem: p-valor muito pequeno significa que:

1)     Ou você obteve um resultado extremamente improvável

2)    Ou a nova droga tem efeito, logo a hipótese de nulidade deve ser rejeitada.

Entenda, por favor: o p-valor não mede “quão certo você está” nem mede “quão importante é a diferença”. O p-valor mede apenas a probabilidade de você errar dizendo que uma  droga tem efeito quando não tem.  Então os pesquisadores querem um p-valor pequeno. Quão pequeno deve ser o p-valor para que você rejeite a hipótese da nulidade? Se p-valor for menor que 0,05, a regra é dizer que o efeito da droga é estatisticamente significante. A escolha do valor 0,05 de probabilidade para rejeitar uma hipótese da nulidade não tem qualquer razão matemática; é apenas um valor que se tornou convencional depois de décadas e décadas de uso.

Vamos pensar mais um pouco: se você tivesse testado a nova droga em uma única pessoa, o fato de ela ter um resfriado de curta duração não provaria nada, mas se o experimento descrito tivesse sido feito com 1.000 pessoas e aquelas que receberam a nova droga tivessem tido resfriados com duração mais curta que os controles, seria razoável acreditar que a nova droga realmente tem efeito sobre  um resfriado.

   Então - como você já deve estar pensando - o p-valor depende tanto do tamanho da amostra como do tamanho do efeito. Portanto, o p-valor tem limitações.  Quanto maior é a amostra, mais seguro é o resultado. Quanto maior é o efeito da intervenção que você está estudando, mais fácil é detectar a significância.

Mas significância estatística não quer dizer resultado verdadeiro, isto é, somente um p-valor pequeno não basta para conferir validade a um trabalho. Um trabalho precisa ter, além da competente análise estatística, bons dados e boas hipóteses em teste. Se a métrica da sua pesquisa estiver errada ou mesmo inadequada, a análise estatística só irá conferir a ela um ar espúrio de respeitabilidade, nada mais. 

Aliás, cabe lembrar que, se os dados são bons e as hipóteses são pertinentes, mesmo com estatísticas inadequadas eles podem ter valor: basta refazer as estatísticas. Isto se faz com artigos publicados em revistas internacionais, quando se suspeita das conclusões. Buscam-se os dados (que devem estar arquivados) e se refazem as estatísticas. Mas nada se pode fazer com dados  incorretos: a boa métrica é crucial.  De qualquer forma, um trabalho só é valido se for válido por inteiro.

Alfa de Cronbach usando SPSS

Pesquisadores que levantam dados por meio de questionários – principalmente, aqueles que constroem seus próprios questionários – devem analisar a confiabilidade do instrumento utilizado. Se você aplicou um questionário uma única vez e foi o único entrevistador, pode avaliar sua confiabilidade calculando o alfa de Cronbach.   

Para isso, comece convertendo as respostas em números –independentemente da quantidade de opções disponíveis em cada item (ou questão) do questionário. A fórmula para calcular do alfa de Cronbach é a mesma, seja para questionários com respostas binárias (como “sim” e “não”) ou respostas escalonadas.

No caso de respostas binárias, você pode atribuir o valor 1 para "sim" e 0 para "não". Para respostas escalonadas, utilize a escala de Likert, que transforma dados qualitativos em valores quantitativos para facilitar a análise estatística. Cada opção de resposta recebe um número e, ao final, é calculado um único resultado para todas as respostas de cada participante.

 Diversos softwares realizam o cálculo do alfa de Cronbach. Aqui, mostraremos como calcular essa estatística, além de algumas outras medidas complementares, utilizando o SPSS. Veja os dados fictícios apresentados na Tabela 1. São 5 questões, feitas a 10 respondentes.

Tabela 1

Resultados da aplicação de um questionário com cinco itens (perguntas) a dez respondentes

As etapas dadas em seguida mostram como avaliar a confiabilidade de um questionário usando o alfa de Cronbach. 

1. Clique em Analisar (Analysis), Escala (Scale), Análise de confiabilidade (Reability Analysis).

                            

   2.  Você será apresentado à seguinte caixa de diálogo:

 

                         

  3.Transfira as variáveis QuestãoA, QuestãoB,... para a caixa “itens” usando o botão 

                                                                         

ou copie todas de uma vez e as transfira para a caixa “Itens”. Veja:                    

                             

4. Em Modelo, clique em "Alfa", que representa o alfa de Cronbach no SPSS. Se você quiser fornecer um título para esta análise, digite-o na caixa Rótulo da escala. O título digitado fica impresso na parte superior da saída do SPSS. Só isso, então você não precisa colocar título (no nosso exemplo, deixamos em branco). Depois, clique em Estatísticas. Você será apresentado à caixa de análise de confiabilidade estatística:

5. Você pode selecionar vários fatores, mas nem pense em selecionar todos. A sugestão é clicar em Resumos, "Médias" e "Correlações". O mais importante, porém, e o "Escalar se o item foi excluído". Clique em "Continuar”. Você retornará à caixa inicial.

6. Clique em OK. Você terá a Saída. 

7.  Veja a Saída (ou Output)

O valor inicial de alfa de Cronbach é 0,748. Esse valor indica uma confiabilidade aceitável, mas não excelente. Em geral, valores acima de 0,7 são considerados adequados, e acima de 0,8 são bons.

Pense um pouco: algum item está reduzindo a confiabilidade? O que acontece se você excluir uma das perguntas? Para responder essas perguntas, olhe as correlações. Vamos aos resultados calculados.

Veja que a questão D tem correlação total de item corrigida menor que as demais. Ela pode estar reduzindo a confiabilidade do questionário, já que sua correlação com os outros itens é fraca. Exclua esse item, para avaliar se o valor de alfa aumenta. Para obter o novo valor de alfa, proceda como anteriormente.

Excluído o item D, o alfa aumentou para 0,842, o que significa que esse item estava reduzindo a confiabilidade do questionário. Isso pode ser explicado pelo fato de o item D não estar bem correlacionado com os demais itens ou porque o padrão de resposta dos respondentes foi muito diferente nele.

Se o objetivo for aumentar a confiabilidade do questionário, pode ser interessante excluir o item D. No entanto, antes de simplesmente removê-lo, vale analisar seu conteúdo:

A questão D mede algo diferente das outras perguntas?

A questão D pode estar mal formulada?

Faz sentido manter a questão por razões teóricas, mesmo que reduza um pouco a confiabilidade?

Finalmente, se você quiser analisar um pouco mais as correlações: na caixa de análise de confiabilidade estatística clique em inter item, correlações. Analise os resultados:

Se houver correlações negativas, pode ser que algumas perguntas estejam invertidas em relação às outras.

Se algum item não se correlaciona bem com os outros, ele pode estar comprometendo o resultado. Remova itens problemáticos

Se as perguntas medem aspectos muito diferentes, o alfa pode ser baixo ou negativo. Rever a lógica das perguntas.

         Veja também

Charles Zaiontz, em Cronbach’s Alpha http://www.real-statistics.com/reliability/cronbachs-alpha/

      Cronbach's Alpha (α) using SPSS Statisticsh ttps://statistics.laerd.com/spss-tutorials/cronbachs-alpha-using-spss-statistics.php        soniavieira.blogspot.com

Regressão Múltipla Usando SPSS: Interprete os Resultados Como Especialista

Você rodou uma regressão linear múltipla no SPSS e… foi recebido com uma avalanche de tabelas? Calma, isso é mais comum do que parece — mas a boa notícia é que você não precisa se perder nos números.

Neste post, vamos direto ao ponto e te mostrar as três tabelas mais importantes da saída do SPSS que todo mundo que analisa regressão múltipla precisa entender. Com explicações claras e exemplo prático, você vai aprender a interpretar os valores de R, R², ANOVA e os coeficientes como um especialista — mesmo que esteja começando agora.

Resumo do Modelo

Para proceder ao cálculo da regressão linear múltipla, vamos utilizar o exemplo dado na postagem anterior (Regressão linear múltipla no SPSS). Os dados estão repetidos na tabela apresentada abaixo.

Com esses dados, obtivemos a primeira tabela de interesse, isto é, a tabela Resumo do Modelo. Esta tabela fornece R, R², R² ajustado e o erro padrão da estimativa, que pode ser usado para determinar quão bem um modelo de regressão se ajusta aos dados.

O valor R é o coeficiente de correlação múltipla. É uma medida da qualidade da previsão da variável dependente, que neste exemplo é o peso da criança, (WGT), dado em libras. Um valor de 0,883 indica bom nível de previsão.

 O valor R² é o coeficiente de determinação. É a proporção de variação na variável dependente explicada pelas variáveis ​​independentes. O valor R² = 0,780 mostra que as variáveis ​​independentes explicam 78,0% da variação da variável dependente, WGT (peso). Você também precisa saber interpretar "R² ajustado", mas vamos explicar isso em próxima postagem.

              Tabela de análise de variância (ANOVA)

A segunda tabela de interesse é a tabela de análise de variância, ou tabela de ANOVA (do inglês, ANOVA table), mostrada em seguida. 

O teste F (indicado como "Z" na tabela ANOVA) avalia o ajuste do modelo de regressão. A tabela mostra que as variáveis independentes (AGE e HGT) predizem significativamente a variável dependente (WGT), já que p < 0,05. Em outras palavras, o modelo de regressão se ajusta bem aos dados.

Coeficientes de regressão

A terceira tabela de interesse é aquela que apresenta os coeficientes de regressão. Veja em seguida.

Coeficientes não padronizados indicam quanto a variável dependente varia com cada variável independente, mantendo-se as demais  constantes. Considere o efeito da idade, neste exemplo: o coeficiente não padronizado para idade (AGE) é igual a 2,050. Isso significa que, para cada aumento de um ano na idade, espera-se um aumento de 2,050 libras no peso (WGT) (lembre-se de que peso está medido em libras).

O teste t, apresentado na tabela, testa se os coeficientes (padronizados ou não) são iguais a zero na população. Se p < 0,05, conclui-se que os coeficientes são significantemente diferentes de zero. Os valores do teste  t e seus respectivos valores p  estão localizados nas colunas "t" e "Sig", respectivamente. Observe que o coeficiente de altura (HGT) é significante.

                                               Conclusão

Foi ajustada uma regressão linear múltipla para prever o peso em função da altura e da idade de crianças. Obteve-se:

         

✅ Apenas a variável altura (HGT) foi significativa ao nível de 5%. A variável idade (AGE), com p = 0,056, pode ser considerada significativa em um nível próximo ao convencional de 5%. Veja a figura na abertura deste post.

Observação

A amostra é muito pequena e composta por dados fictícios. Portanto, as conclusões não são válidas na prática. Este exemplo foi utilizado apenas para facilitar os cálculos e fornecer uma referência importante ao leitor (KLEINBAUM e KUPPER). Os dados não foram convertidos para o sistema métrico decimal porque resultariam em valores não inteiros, o que dificultaria a digitação.

Ajuste Sua Primeira Regressão Linear Mltipla no SPSS

                                                 Análise de regressão

A análise de regressão permite estabelecer um modelo para descrever a relação entre duas ou mais variáveis. Trata-se de uma técnica que possibilita fazer previsões sobre uma variável – chamada variável resposta (dependente) – com base em informações obtidas de outras variáveis – conhecidas como  variáveis explicativas (também chamadas de explanatórias, preditoras ou independentes).

Regressão linear simples

A regressão linear simples é denominada “linear” porque o modelo ajustado é uma reta, e “simples” porque há apenas uma variável explicativa. A regressão linear simples é definida pelo modelo:

 

Nesse modelo, os pares de variáveis Y_i e X_i (i=1, 2, ..., n) representam a variável resposta e a variável explicativa, respectivamente; b₀ e b₁ são parâmetros a serem estimados a partir dos dados e e_ij  (i=1, 2, ..., n) são erros aleatórios.

Por exemplo, ao analisar um conjunto de dados de peso e altura de jovens que se apresentaram para o serviço militar, pode-se supor que peso seja função linear da altura. Ajustando uma reta a esses dados, obtém-se as estimativas b₀ e b₁ dos parâmetros b₀ e b₁ da regressão.

 O termo b₀ é o coeficiente linear, também conhecido como intercepto (intercept, em inglês) e o termo b₁ é o coeficiente angular, também conhecido como inclinação (slope, em inglês). A reta ajustada aos dados, considerada a melhor, no sentido de possuir propriedades estatísticas desejáveis, é chamada de reta de regressão. Muitos autores também a denominam reta de mínimos quadrados, em referência ao método estatístico utilizado para calcular as estimativas.

Regressão linear múltipla

A regressão linear múltipla (multiple linear regression) é uma técnica estatística que usa diversas variáveis ​​explicativas para prever a variável resposta. Logo, a regressão linear múltipla estabelece o modelo para uma relação linear entre a variável resposta (dependente) e diversas variáveis ​​explicativas (independentes).

Nessa fórmula, Y_i (i =1, 2,...,n) são as n observações da variável resposta (dependente) e X_i1, X_i2,...,X_ik  são as n observações das k variáveis explicativas (independentes). O coeficiente b₀ é o intercepto e b₁, b₂,..., b_k  são os coeficientes angulares correspondentes a cada variável explicativa. Os termos e_i são os erros do modelo.

Para ajustar um modelo de regressão linear múltipla, algumas pressuposições deve ser atendidas.

Pressuposições

🔸A variável resposta (dependente) deve ser contínua.

🔸Deve haver uma relação linear entre a variável resposta e cada uma das variáveis explicativas.

🔸As observações das variáveis explicativas devem ser independentes entre si.

🔸Os desvios devem ter distribuição normal de média zero e variância s².

Vamos mostrar, por meio de um exemplo, como ajustar uma regressão linear múltipla a um conjunto de dados utilizando o SPSS (Statistical Package for Social Sciences). Em outra postagem, explicaremos como interpretar os resultados.

                                                                  Exemplo

Considere uma amostra aleatória de 12 crianças atendidas em uma clínica. O peso, a altura e a idade dessas crianças estão apresentados abaixo, já formados para inserção no SPSS. O peso (weight) está em libras, a altura (height) em pés e a idade (age) em anos completos. Nosso objetivo é estudar o peso em função da altura e da idade.         

                  Como realizar a análise de regressão linear múltipla no SPSS

As etapas dadas em seguida mostram como realizar a análise de regressão linear múltipla no SPSS, supondo que todas as pressuposições do modelo foram atendidas. Ao final, exibiremos os resultados da regressão. 

🔸   No menu principal do SPSS, clique em Analisar > Regressão > Linear.

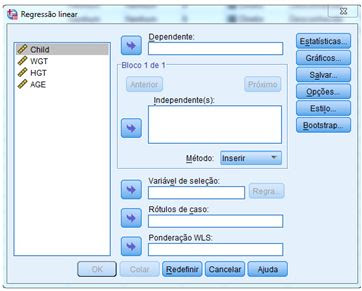
🔸  Você será apresentado à caixa de diálogo.

🔸 Transfira a variável dependente peso (WGT) para a caixa “Dependente” e as variáveis independentes altura (HGT) e idade (AGE) para a caixa “Independente” utilizando o botão de transferência apropriado.

🔸  Clique em Estatísticas. Na caixa de diálogo que se abrirá, selecione as opções Estimativas e Ajuste do Modelo.

   🔸 Clique em Continuar para retornar à caixa de diálogo principal da Regressão linear. 

       🔸 Clique em OK. Será gerada a Saída, com os resultados. 

✅ Saída dos Resultados