Uma das principais finalidades da
Estatística é estimar propriedades desconhecidas da população. Tais
propriedades são, necessariamente, numéricas:
médias, proporções etc. Essas estimativas devem ser obtidas a partir de amostras aleatórias, se o objetivo do
pesquisador for realizar inferência estatística.
Neste post, vamos apresentar a Função de Distribuição Empírica (Empirical Distribution Function – EDF), um estimador diferente e bastante útil, além de mostrar como aplicá-la no Teste de Aderência de Kolmogorov.
O que é a Função de Distribuição Empírica (EDF)?
A
verdadeira função de distribuição de uma variável aleatória é geralmente desconhecida. Porém, podemos ter alguma
ideia de qual seria essa função e usá-la como aproximação
da função verdadeira.
Para
isso, observe uma amostra da variável aleatória ,
ou seja: X. A
partir dessa amostra, você pode construir um gráfico chamado ,
que é a função de distribuição empírica, e
usá-lo como estimativa da função de
distribuição de .
Exemplo: Como construir a EDF?
Considere
o tempo de corrida (em minutos) de cinco pessoas em determinado percurso:
6,23 –
5,58 – 7,06 – 6,42 – 5,20
Passos para construir o gráfico:
1.
Coloque
os dados em uma planilha e ordene-os.
2.
Na
coluna ao lado, escreva a proporção acumulada
de cada dado. Como ,
cada dado representa .
Tabela 1
Função de distribuição empírica S(x)
3.
Construa
um gráfico com os valores observados no eixo X e
as proporções acumuladas no eixo Y.
Figura 1
A função de distribuição empírica S(x) representa o
número de valores amostrais menores ou iguais a x. Note que S(x) depende da
amostra: outras amostras gerarão gráficos diferentes. Isso evidencia a natureza
aleatória de S(x).
Tecnicamente, S(x) pode ser vista como uma função
aleatória. Os valores observados produzem gráficos, e não números. S(x) é
uma função de distribuição empírica que estima a verdadeira função de
distribuição da variável aleatória (chamada aqui de F(x)), para distingui-la de S(x).
Objetivo
Verificar se os dados seguem uma
determinada distribuição conhecida, usando a função empírica
e comparando-a com uma função teórica
Hipóteses
Seja F*(x) uma função de distribuição conhecida que você assumiu como sendo a de seus dados. Para um teste bilateral, sua hipótese é:
H0: F(x)
= F*(x) para
todo x, de - ∞ a + ∞.
H1: F(x) ≠ F*(x) para pelo menos um valor de x.
Estatística de teste
A estatística do teste mede a maior diferença vertical entre
S(x) e F*(x). S(x) é a função de
probabilidade acumulada dos dados. A estatística de teste depende da hipótese
formulada.
T=sup ∣F∗(x)−S(x)∣
Lê-se: “T é igual ao supremo do valor absoluto da
diferença F∗(x)−S(x) para todo x”.
Regra de decisão
Rejeite H0 no nível de significância α se T exceder
w1−α, dado na tabela
que está no final do post. Essa tabela é exata somente se F∗(x) for
contínua; caso contrário, o teste será conservador.
EXEMPLO
Foram obtidos os seguintes dados:
A hipótese é a de que a função de distribuição é uniforme.
A função de distribuição acumulada está na Figura 2:
F∗(x) = 0 para x<0
F*(x)
= X para x<0≤x<1
F*(x)
= 1 para x≤1
Figura 2
Função de
distribuição uniforme F(x*)
Formalmente:
H0: F(x)
= F*(x), para
todo x, de - ∞ a + ∞.
H1: F(x)
≠ F*(x) para
pelo menos um valor de x.
em que F(x) é a função de distribuição desconhecida
e F∗(x) refere-se à distribuição uniforme já definida.
Para um teste bilateral com nível de significância
α = 0,05 (logo, p = 1−α = 0,95), para n=10, a região de rejeição
corresponde a valores de T maiores do que 0,409.
O valor de T é obtido no gráfico que apresenta a
função de distribuição empírica S(x) sobreposta à função de distribuição F∗(x),
conforme a hipótese.
Figura 3
A maior distância vertical entre os gráficos é
0,290 (em vermelho na Figura 3), quando x=0,710.
Veja que, para x=0,710, a função de distribuição
acumulada F∗(x)=x=0,710. Para x=0,710, a função de distribuição acumulada S(x)=1,00.
Escreve-se:
T=∣0,710−1,00∣=0,290
Como T=0,290 é menor que 0,409, não se rejeita a
hipótese da nulidade.
Conclusão
A função de distribuição empírica
S(x) é uma
ferramenta poderosa para estimar distribuições e realizar testes como o de
Kolmogorov. Sua natureza aleatória ressalta a importância da amostragem e da
comparação visual e numérica com funções teóricas.








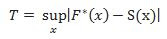





No comments:
Post a Comment