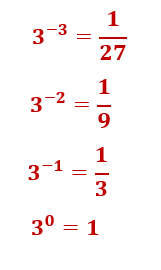Qualquer número à potência zero

📌 Por que qualquer número elevado à potência zero é igual a 1?

Para entender isso, comece lembrando uma das regras das potências, ou seja, a divisão de potências de mesma base:

                                

                              ✏️ Veja um exemplo:

                          

Mas sabemos que:

                                         

é igual a 1, porque o numerador é igual ao denominador. Aplicando  a lei dos expoentes, vem:

                                          

           Logo:

                                             4⁰=1.

✅ Regra geral:

                 Para qualquer número a≠0, temos:

                          

📜 Outra maneira de pensar

Vamos analisar este exemplo:

                                 

E, aplicando a regra da divisão:

                                 

Agora veja:

                                  

Como o numerador e o denominador são iguais, o resultado é 1. Então:

                                

                            

✅ Regra geral:

                 Para qualquer número a≠0, temos:

                                                    a⁰=1.   

📜 Pensando com uma sequência de potências

Considere a sequência:

                           3¹; 3²; 3³; 3⁴; 3⁵; 3⁶…

Os valores são:

                                   3; 9; 27; 81; 243;729 …

Observe o padrão: indo para a direita, multiplicamos por 3,indo para     a esquerda, dividimos por 3. Vamos voltar até o expoente zero:

              …3^-6; 3^-5; 3^-4; 3^-3; 3^-2; 3^-1; 3⁰; 3¹; 3²; 3³; 3⁴; 3⁵; 3⁶…

  

                  

Calculando:​                                               

​

Dividindo por 3 a cada passo, ao chegar em 303^030, temos:

                          
✅ Conclusão: Para manter o padrão da sequência, 3⁰ precisa ser igual a 1.

❓ E quanto vale 0⁰ ?

Aqui entram duas regras diferentes:

                 1. Se a base for zero e o expoente for maior que zero, então:

                                              0⁵ = 0.

                 2. Se a base for diferente de zero e o expoente for zero:

9⁰ = 1

Então, o que acontece com 0⁰ ? Ele parece poder ser 0 ou 1. Mas…

✅ Resposta:
0⁰  é considerado indeterminado.

Essa é uma convenção matemática, porque atribuir um valor 0⁰ depende do contexto — especialmente em limites e análise matemática. Em muitas situações práticas, considera-se,  por conveniência e consistência com as leis das potências, 0⁰=10⁰=1  mas formalmente dizemos que é uma indeterminação.

---

🔎 Nota final:

Este texto foi inspirado nas explicações do The Math Forum:

🔗 http://mathforum.org/dr.math/faq/faq.number.to.0power.html

 

Descomplicando as Leis da Potenciação

Multiplicação de potências de mesma base

Você já sabe que o expoente de um número diz quantas vezes esse número deve ser multiplicado por ele mesmo.

                                           

Exemplo

 Quando você lê 3², sabe que o expoente 2 diz para multiplicar 3 por si mesmo duas vezes.

                  3² = 3 x 3 = 9

Mas em a^maⁿ, quantas vezes o número a deve ser multiplicado por si mesmo? É fácil: multiplique o número a por si mesmo m vezes e depois, mais n vezes. Então o número a foi multiplicado por si mesmo m+n vezes. Logo:

Para multiplicar potências de mesma base: mantenha a base e some os expoentes.

                       

Divisão de potências de mesma base

     Genericamente, a divisão de potências de mesma base pode ser escrita como segue:

              

                  

                Para dividir potências de mesma base:

mantenha a base e subtraia os expoentes.

                                 

                                                   Potência de um produto

         O produto de dois ou mais fatores pode ser elevado a uma potência.

  

Potência de produto:

o produto de dois ou mais fatores elevados ao um  expoente é igual ao produto desses fatores, cada qual elevado ao mesmo expoente.

                            

                             Potência de uma divisão

       Uma divisão elevada à determinada potência pode ser indicada como segue:

Potência de divisão:

o resultado de uma divisão elevada a um expoente é dada por dividendo e divisor elevados ao mesmo expoente.

                                 

Potência de potência

           Genericamente, potência de potência pode ser indicada como segue:

Potência de potência:

o resultado de uma potência elevada a outra potência é dada pelo produto dos expoentes.

Mesma base: $a^m \cdot a^n = a^{m+n}$

Mesmo expoente: $a^m \cdot b^m = (ab)^m$

Potência de potência: $(a^m)^n = a^{mn}$

Divisão com mesma base: $\frac{a^m}{a^n} = a^{m-n}$

Potência de fração: $\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}$