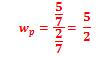Estatística para Ciências Sociais: EXEMPLOS

1. Média, mediana e moda são...?

1. Medidas de significância estatística.
2. Medidas de tendência central.
3. Medidas de desvio padrão.
4. Medidas de erro padrão.

2. Um pesquisador quer estudar os efeitos da música alta na aprendizagem. Um grupo de 30 alunos é selecionado para participar do estudo. O grupo de estudantes é...?

                                                            

1. A população.
2. A variável independente.
3. O desvio padrão.
4. A amostra.

3. Qual das seguintes opções não é uma estatística descritiva?

1.  A renda média de um homem americano de 25 anos é de US $ 22.000 por ano.
2.  Em 2011, 91% das mortes no local de trabalho aconteceram com homens.
3.  Os consumidores gastaram US $ 1,2 bilhão em smartphones no ano passado.
4.  Fumar aumenta a chance de morrer em 37%.

4. Qual das frases mais bem descreve correlação?

1.  É um método para determinar a probabilidade de um resultado futuro específico.
2.  É um método para descobrir relações causais.
3.  É um método para medir o grau de relação entre variáveis.
4.  É um método para analisar diferenças entre os grupos.

5. A média de uma distribuição de dez escores é 6. Existem dois escores na distribuição que são iguais a 6. Você os remove. A média  agora é:

1.  Maior que 6.
2.  A mesma.
3.  Menor que 6.
4.  Não há dados suficientes para saber.

6. O que é uma amostra aleatória?

1. Um conjunto de unidades retiradas de uma população onde algumas unidades têm maior probabilidade ​​do que outras de serem tomadas para a amostra.
2.  Um conjunto de unidades retiradas de uma população de forma não estruturada.
3.  Um conjunto de unidades retiradas de uma população onde cada unidade da população tem probabilidade aleatória de compor a amostra.
4.  Um conjunto de unidades retiradas de uma população onde cada unidade na população tem a mesma probabilidade de compor a amostra.

7. O que é amplitude de uma distribuição?

1.  A distância entre o menor e o maior valor.
2.  A distância entre a média e o maior valor.
3.  A distância entre a moda e o valor mais alto.
4.  A distância entre a mediana e o valor mais alto.

8. Um pesquisador classifica o estresse dos participantes de uma pesquisa em uma escala de 0 a 10. Qual é o nível de medição?

1.  Discreta.
2.  Ordinal.
3.  Nominal.
4.  Contínua.

9. Se, em um teste, você tiver nota igual ao 40º percentil...

1. 40% das pessoas tiveram nota igual maior que a sua.
2.  Sua nota no teste foi 60%.
3.  O resultado do teste foi de 40%.
4.  40% das pessoas tiveram nota igual ou menor que a sua.

10.  Um pesquisador está analisando o efeito do cansaço físico sobre o resultado dos alunos em uma prova. Qual é a variável dependente?

1.  O tamanho da amostra do estudo.
2.  O nível da variável de cansaço.
3.  O grupo de controle.
4.  O resultado dos alunos em uma prova.

As questões (e as respostas) deste teste você encontra, em inglês, em

http://www.socscistatistics.com/quizzes/Default.aspx

O teste pretende ser um auxílio de estudo para estudantes das ciências sociais e humanas, seguindo o conteúdo padrão dos programas de estatística desses cursos nos Estados Unidos. Se quiser, me pergunte as respostas.

Teste de Kruskal-Wallis não compara médias

O teste de Kruskal-Wallis é também conhecido como análise de variância de Kruskal-Wallis, ANOVA de Kruskal-Wallis, ANOVA não paramétrica. Talvez essa nomenclatura, reportando o teste de Kruskal-Wallis à análise de variância e ao F de Snedcor, faça com que muitos se confundam e pensem que o teste de Kruskal-Wallis compara médias. Errado.

O teste de Kruskal-Wallis não trabalha com hipóteses sobre os parâmetros. Não testa, portanto, a hipótese a igualdade de médias, nem testa a igualdade de medianas. O teste de Kruskal-Wallis é indicado para testar a hipótese de que três ou mais populações têm igual distribuição.

Logo, quando se aplica um teste de Kruskal-Wallis, não devem ser apresentadas médias, medianas ou gráficos com essas estatísticas. O teste de Kruskal-Wallis trabalha com postos – não com dados coletados.

Para deixar isso claro, é apresentado um exemplo bastante engenhoso[1] que compara três grupos. O resultado do teste de Kruskal-Wallis é significante (p-valor = 0,025). No entanto, os três grupos têm a mesma média (43,5) e mesma mediana (27,5). Apresentar as médias ou as medianas dos três grupos seria enganoso. Afinal, essas estatísticas – além de não estar em teste – não mostrariam que as distribuições são diferentes. Os postos médios são diferentes: 34,6; 27,5 e 20,4, respectivamente. Eles é que devem ser apresentados.

---

[1] MCDONALD, JH. Handbook of Biological Statistics. Baltimore. Sparky House Publishing, 2nd ed. p. 165-172, 2009.

Odds ratio (razão de chances)

 Não confunda probabilidade com chance! Embora as duas palavras nos remetam à ideia de uma medida do possível, elas não dão medidas iguais.

Exemplo

  Você joga um dado. Ganha se sair o número 6. Qual é a probabilidade de você ganhar?

   Quais são suas chances nesse jogo?

                                        1 : 5

       ou seja, espere perder cinco vezes para cada vez que               ganhar.

Probabilidade é a fração do número de tentativas que devem ser feitas para que se possa esperar determinada ocorrência.

Chance mostra a razão entre o número de vezes que se espera um evento ocorrer e o número de vezes em que esse evento não ocorrerá.

 

  No exemplo, a probabilidade mostra que você deve esperar o número 6 em 1/6 dos lançamentos. Já a chance diz que você terá “um” numero 6 para “cinco” que não são 6.

   Muito cuidado, também, ao comparar valores de probabilidades e de chances ¹. Uma probabilidade de 9/10 é bem alta, mas uma chance de 9: 10 é baixa. Será? Veja bem:

   Probabilidade de 9/10 significa que você “acerta” 9 de 10 tentativas. Chance 9:10 significa que, para 9 que você “acerta”, erra 10. Pense bem: probabilidade 9/10 significa chance de 9:1. Difícil? Mas existe uma fórmula para calcular chance.

Por definição, chance, que indicaremos por w, é a razão entre a probabilidade de determinado evento ocorrer (p) e a probabilidade (q) de esse evento não ocorrer.

                                                  

  Evidentemente,

                             p + q = 1.

Exemplo

 Lembre-se dos primeiros experimentos de Genética, conduzidos por Mendel: ervilhas verdes cruzadas com ervilhas amarelas produzem ervilhas amarelas, que cruzadas entre si segregam na proporção de três amarelas para cada verde.

   Então, a probabilidade de ocorrer ervilha amarela quando se cruzam ervilhas amarelas heterozigotas é

e a probabilidade de ocorrer ervilha verde é

                   

A chance é

 O interesse da pesquisa é estabelecer comparações que possam ser feitas de diversas maneiras. Para comparar as chances de determinada ocorrência em dois grupos, é comum calcular a razão de chances (odds ratio).

Razão de chances, que indicaremos pela letra o (de odds), é definida pela fórmula:

                        

    A razão de chances (OR) é uma das várias estatísticas que se tornaram muito importantes na pesquisa clínica e na tomada de decisões. É particularmente útil porque fornece informação clara aos clínicos sobre qual é o tratamento que tem as melhores chances de beneficiar o paciente.

Exemplo 

 Vinte amigos vão a uma lanchonete para uma comemoração: 7 pedem um sanduíche a base de peixe, 13 pedem um sanduíche a base de carne ². Dos 7 que comeram peixe, 5 se sentiram mal depois e dos 13 que comeram carne, 3 se sentiram mal. Compare as chances de passar mal, dos dois grupos.

Chance de passar mal com o sanduíche de peixe

 

Chance de passar mal com o sanduíche de carne

                           Razão de chances

    

O que isto significa?   Quem consumiu peixe teve 8,33 vezes mais chance do  efeito adverso. Mas muita atenção aqui:

                 Associação não significa causa!

   1. Probability vs. Odds Ratio - Math Forum - Ask Dr.Math    mathforum.org/library/drmath/view/71943.html

  2.  https://beanaroundtheworld.wordpress.com/2011/10/07/epidemiology-odds-ratio-or/ 

Por que usamos "n - 1" na variância? Um exemplo simples explica

RESUMO: Um exemplo simples com bolas numeradas ajuda a entender por que usamos "n - 1" na variância e como surge o erro padrão da média. Inclui gráficos para facilitar a visualização.

Para explicar o erro padrão da média e apresentar a lógica dos graus de liberdade associados à variância da amostra, vamos usar um exemplo irreal — mas útil para compreender esses conceitos.

Imagine uma urna contendo três bolas numeradas: 4, 10 e 16. Um jogador retira uma bola, anota o número, retorna a bola à urna e faz uma nova retirada. Novamente, anota o número e retorna a bola. Em seguida, calcula a média dos dois números obtidos, que será sua pontuação no jogo.

Do ponto de vista teórico, temos uma população infinita de bolas numeradas (já que a bola é devolvida à urna após cada retirada), e esse   jogo pode ser repetido indefinidamente. A média populacional μ da variável em estudo é:

Como _​  pode assumir os valores 4, 10 ou 16, todos com probabilidade ​,  temos:                                              

                                                            

É importante notar que temos a média m da população, que é um parâmetro. Portanto, a variância populacional associada a essa média não envolve graus de liberdade. A dispersão da variável em torno da média m é dada por:                                   

                             

No caso do exemplo:

Vamos agora analisar os possíveis resultados do jogo. Como tanto a primeira quanto a segunda retirada podem resultar em 4, 10 ou 16, temos 9 combinações possíveis. A Tabela 1 mostra todas essas amostras de tamanho 2, suas médias e variâncias. 

Tabela 1

 Amostras de dois números que podem ser obtidas da população constituída por números 4, 10 e 16, com as respectivas médias e variâncias

Ao observar a Tabela 1, notamos dois fatos importantes: 

1.    A média das médias de todas as amostras possíveis é igual à média da população.

2.   A média das variâncias de todas as amostras possíveis é igual à variância da população, desde que as variâncias das amostras tenham sido calculadas com o divisor n−1 (isto é, com a variância amostral).

Dizemos, então, que:

🔺A média de uma amostra é uma estimativa não tendenciosa da média populacional.

🔺A variância de uma amostra (com divisor n−1) é uma estimativa não tendenciosa da variância populacional.

🔔 Por que "não tendenciosa"? Porque essas estimativas tendem, em média, aos valores verdadeiros dos parâmetros da população.

No nosso exemplo, as médias das amostras têm diferentes probabilidades:

🔸 Médias 4 e 16, cada uma ocorre 1 vez : probabilidade 1/9

🔸 Médias 7 e 13, cada uma ocorre 2 vezes: probabilidade 2/9​

🔸 Média 10, ocorre 3 vezes: probabilidade 3/9

A fórmula da média das médias ponderada pelas probabilidades é:

                                                  

Substituindo os valores da Tabela 1:

                        

Como as médias das amostras estão distribuídas em torno da média populacional, podemos medir essa dispersão: é a variância da média dada por:

                                

Substituindo os valores da Tabela 1:  

 

🔔 Na prática, porém, não temos acesso a todas as amostras possíveis — o pesquisador normalmente dispõe de apenas uma amostra. Mesmo assim, é possível estimar a variância da média por meio da por meio da fórmula:

                                                                                                            

Onde:

· s² é a variância da amostra (calculada com divisor n−1),

· n é o tamanho da amostra.

Essa fórmula permite estimar a variabilidade esperada da média da amostra, caso o estudo fosse repetido várias vezes. O desvio padrão da média, conhecido como erro padrão da média, é então:

Portanto, erro padrão da média é a raiz quadrada com sinal positivo da variância da média.

Esse valor nos diz o quanto a média obtida em uma amostra pode variar em torno da verdadeira média populacional, sendo fundamental para construções de intervalos de confiança e testes de hipóteses.

                                      🟩 Conclusão

O exemplo simples que desenvolvemos, com bolas numeradas e todas as combinações possíveis de amostras, mostra como conceitos muitas vezes abstratos na estatística — como erro padrão da média, variância amostral e graus de liberdade — têm uma base lógica clara e visual. Ao calcular todas as médias e variâncias possíveis, conseguimos entender por que a média amostral é uma boa estimativa da média da população e por que a variância deve ser dividida por n−1n - 1n−1 para não subestimar a variabilidade real.

Mais do que decorar fórmulas, é importante compreender a intuição por trás delas. E nada melhor do que um exemplo pequeno e completo, acompanhado de gráficos, para transformar teoria em compreensão.