O Teste de Bonferroni Protege as Conclusões nas Comparações de Médias Duas a Duas

As análises de variância (ANOVA) são muito frequentes na literatura científica, sempre seguidas por testes de comparação de médias. No entanto, é comum que os autores não expliquem por que escolheram determinado teste nem mencionem as limitações associadas à escolha. Em muitos trabalhos, o teste utilizado sequer é citado.

Neste post, trataremos das comparações a posteriori (ou não planejadas, unplanned comparisons) de médias duas a duas, utilizando testes paramétricos. Tais testes baseiam-se nas distribuições t, F ou q (amplitude studentizada). Nenhum deles é universalmente superior aos demais — cada um tem seus prós e contras.

O teste LSD de Fisher

O teste mais simples é o LSD de Fisher (least significant difference), que utiliza a distribuição t com os graus de liberdade do quadrado médio do resíduo da ANOVA. É um teste poderoso, mas fixa o erro tipo I por comparação (comparisonwise Type I error rate). Quando usado para múltiplas comparações entre grupos, o erro tipo I global (experimentwise error rate) aumenta rapidamente.

Por isso, Fisher recomendou que o LSD fosse aplicado apenas quando o teste F da ANOVA for significante — o chamado LSD protegido.

Ajuste de Bonferroni

O ajuste de Bonferroni é uma forma simples e conservadora de controlar o erro tipo I global. A ideia é a seguinte: se há m comparações a serem feitas, e se desejamos manter o nível de significância do experimento em α, então devemos aplicar cada teste com um nível de significância α/m.

Exemplo ilustrativo

Considere três grupos: A, B e C. As comparações possíveis são:

·     A × B

·     A × C

·     B × C

Total: m = 3 comparações.

Se o nível de significância do experimento é α = 0,05, então cada comparação deve ser testada com 

                                          αajustado = α/m = 0,05/3 ≈ 0,0167.

Com isso, garantimos que a probabilidade de cometer pelo menos um erro tipo I em todas as comparações será, no máximo, α.

Como aplicar o teste de Bonferroni

1.   Calcule o número total de comparações m=k(k−1)2, onde k é o número de grupos.

2.   Determine o nível ajustado de significância:

3.   Realize os testes duas a duas, usando esse novo nível de significância.

4.   Compare as diferenças entre as médias: considere significativas aquelas cujos valores absolutos ultrapassarem o limite calculado.

Exemplo aplicado

A Tabela 1 apresenta os dados de um ensaio fictício com seis tratamentos, medindo a redução da pressão arterial (em mmHg) ao longo do tempo.

Tabela 1. Diminuição da pressão arterial segundo o tratamento

A análise de variância desses dados resultou em um F significante (ver Tabela 2), indicando diferenças entre as médias.

Tabela 2. Resultados da ANOVA

Como o F foi significante, procedemos às comparações duas a duas pelo teste de Bonferroni. Para k = 6, o número de comparações possíveis é

Com α = 0,05, o nível de significância por comparação será:

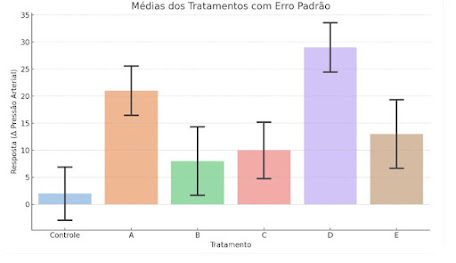
A Tabela 3 apresenta as comparações de médias duas a duas, com asterisco (*) indicando diferenças significantes no nível de significância ajustado. Veja também a Figura 1, que ajuda na percepção das diferenças.

Tabela 3. Comparação de médias pelo teste de Bonferroni

Figura 1. Comparação de médias pelo teste de Bonferroni

LIVROS