Probability in Reverse: Bayes' Theorem

 

Before presenting Bayes' theorem, it’s helpful to recall the definition of conditional probability to highlight the difference between this concept and the theorem itself.

❗ Definition

The conditional probability of an event B given that event A has occurred is the chance of B happening under the condition that A has already occurred. It is denoted by P(B∣A), read as “the probability of B given A”.

                                                

       Key points:

   🔸 A and B are dependent events.
   🔸 Event A occurs before event B.

🛑 Example

An urn contains five balls that differ only by color: two red and three blue. Two balls are drawn without replacement, one after the other.

Question: What is the probability that the second ball is red, given that the first was blue?
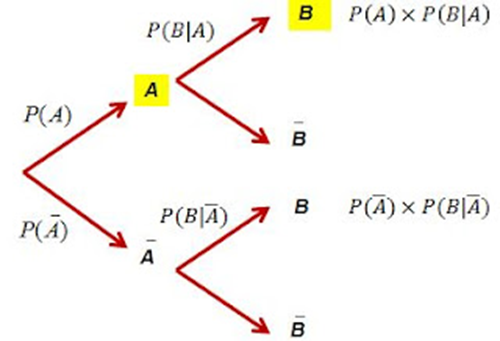
A tree diagram helps visualize the possible outcomes in this situation. All conditional probabilities are shown, and the answer to the question is highlighted in yellow.

       The answer is obtained using the multiplication rule for dependent events.

                                                           

     Answer:  The probability that the second ball is red, given the first was blue is 3/10, ou 30%.

        Now that we understand conditional probability, let’s see how Bayes’ Theorem allows us to '                    reverse' the condition.

❗ BAYES' THEOREM

⚠️ P(B∣A) and P(A∣B) may look similar, but they represent different ideas. Consider the following examples:

1. Let A = “has technical training”; B = “performs good service”.
     🔸 P(B∣A): probability of performing good service given technical training.
     🔸 P(A∣B): probability of having technical training given that good service was performed.

2. Let A = “was a good student in high school”; B = “passed the college entrance exam”.
    🔸 P(B∣A): probability of passing the exam given that the person was a good student.
    🔸 P(A∣B): probability of having been a good student given that the person passed the exam.

These pairs of probabilities often appear in real-life problems. Now let’s find a formula to calculate P(A∣B). From:

      we can write:

     and we have

Bayes’ Theorem:

🔔 Interpretation

Bayes’ Theorem reverses the order of information:

• Conditional probability deals with P(B∣A): probability of B occurring given A occurred.

• Bayes’ Theorem addresses P(A∣B): probability of A occurring given B occurred — that is, the reverse of conditional probability.

🛑 Example – Applying Bayes’ Theorem

Let’s revisit the urn example, but now with a different question:

Question: What is the probability that the first ball drawn was blue, given that the second was red?

  From the tree diagram, we see that the second ball being red can happen in two ways:

                        • Blue then Red (B–R)
                        • Red then Red (R–R)

  The event of interest is: first blue given second red.

    We apply Bayes’ Theorem:

                              

Answer: Using Bayes’ Theorem, the probability the first ball was blue given the second is red is 3/4, ou 75%.

🛑 Example – Breathalyzer Test

In a city, the breathalyzer test is mandatory.
         • 25% of drivers drink before driving.
         • Of those who drink, 99% test positive.
         • Of those who do not drink, 17% also test positive.

Question: If a driver tests positive, what is the chance they actually consumed alcohol?

Let the events be:
          • B: drinks
          • NB: does not drink
          • + : positive test

Compute P(B∣+) using the given data.

             

       Answer: If a driver tests positive,  the chance they actually consumed alcohol is 66%.

    🛑 Example – Horse Race

       Two horses race: White and Black.

                  • In 12 previous races, White won 5 times and Black 7.
                 • In 3 of White’s 5 victories, it was raining.
                 • In 1 of Black’s 7 victories, it was also raining.

       Question: It is raining now. What is the probability that White will win?
      

        Compute P(White wins∣rain)

     Answer: The probability that White wins is 3/4 ou 75%.

        CONCLUSION: 

• "Bayes’ Theorem is powerful because it lets us update probabilities with new evidence. Remember: it ‘reverses’ the condition!"