Teorema de Bayes: exemplos

EXEMPLO 1

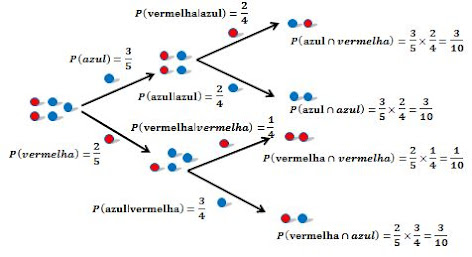
1.    Uma caixa contém duas bolas vermelhas e três bolas azuis. Duas bolas são retiradas ao acaso, uma em seguida da outra e sem que a primeira tenha sido recolocada.

a) Qual é a probabilidade de a segunda (evento B) bola retirada ser vermelha sob a condição de a primeira (evento A) bola retirada ser azul?

b) Qual é a probabilidade de a primeira (evento A) bola retirada ser a azul sob a condição de a segunda (evento B) ser vermelha?

A primeira questão pede uma probabilidade condicional:

A segunda questão deve ser tratada pelo teorema de Bayes: 

EXEMPLO 2

·       Qual é a probabilidade de um motorista estar alcoolizado e causar um acidente de trânsito?

·         Qual é a probabilidade de um motorista causar acidente de trânsito dado que está alcoolizado?

Para resolver problemas que envolvem eventos dependentes que ocorrem em sequência, é importante saber a sequência. No exemplo, estão propositalmente postas as duas sequências possíveis. Então: motorista estar alcoolizado (evento A) e motorista causar acidente de trânsito (evento B).

 

 A primeira questão pede uma probabilidade condicional:

 A segunda questão deve ser tratada pelo teorema de Bayes: 

 EXERCÍCIOS

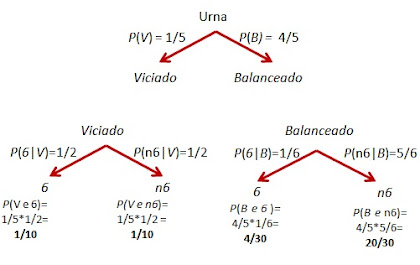
EXERCÍCIO 1: Uma urna contém cinco dados: quatro são balanceados, mas em um deles a probabilidade de ocorrer face “seis” é o triplo da probabilidade de ocorrer face “um”. As demais faces têm igual probabilidade de ocorrer. Um dado retirado da urna ao acaso é lançado. Qual é a probabilidade de esse dado ser balanceado se sair “seis”?

Dica: aplique o teorema de Bayes.

EXERCÍCIO 2: Uma urna contém cinco bolas: duas são vermelhas, três são azuis. Uma segunda urna contém sete bolas: três são vermelhas, quatro são azuis. Retira-se uma bola ao acaso de uma das urnas. Qual é a probabilidade de que essa bola, se for da cor azul, ter sido retirada da primeira urna?

EXERCÍCIO 3: Em uma cidade em que os carros são testados para emissão de poluentes, 25% deles emitem quantidade considerada excessiva. O teste falha para 99% dos carros que emitem excesso de poluentes, mas resulta positivo para 17% dos carros que não emitem quantidade excessiva. Qual é a probabilidade de um carro que falha no teste realmente emitir quantidade excessiva de poluentes?

EXERCÍCIO 4: A probabilidade de diagnosticar corretamente determinada doença rara é 0,70. Quando diagnosticada corretamente, a probabilidade de cura é 0,90. Se não for diagnosticada corretamente, a probabilidade de cura é 0,40.Se o paciente com a doença é curado, qual é a probabilidade de que tenha sido diagnosticado corretamente?

RESPOSTAS

EXERCÍCIO 1

Vamos indicar por B dado balanceado e por V dado viciado. Vamos indicar face “seis” por 6 e as outras faces por n6. Então:

EXERCÍCIO 2:

Fica mais claro assim?

EXERCÍCIO 3:

EXERCÍCIO 4:

   

Veja

1.       Maher, Patrick https://www.google.com.br/?gws_rd=ssl#q=Howson+2+Bayes%27s+Theorem+(pp.+13--26)+-+Patrick+Maher

2.       Freund JE & Smith, RM Statistics: a first course.Englewood Cliffs, Prentice Hall, 4ed. 1986. P 177.

Teorema de Bayes na Genética

A distrofia muscular de Duchenne (DMD) progride rapidamente. Causa degeneração dos músculos e morte prematura. A causa principal da doença é uma mutação (alteração) em um gene chamado DMD, recessivo, localizado no cromossomo X. É, portanto, uma doença ligada ao sexo.

Se uma pessoa de sexo masculino tem o gene DMD, provavelmente manifestará a doença, mas para que uma mulher manifeste a doença é necessário que seja homozigota para esse gene recessivo.

No entanto, mulheres portadoras de mutação no gene DMD têm 50% de chance de transmitir esta alteração para seus filhos em cada gestação. Veja o heredograma, em que X’ representa o gene com mutação. Então:

·      portadoras estão indicadas por X’X,

·      não portadoras por XX,

·      homens sem a mutação no gene por XY,

·      homens com a mutação por X’Y.

                          Exemplo

Uma mulher (vamos chamá-la de Maria) pergunta a probabilidade de ser portadora do gene para a distrofia muscular de Duchenne. Como um seu irmão e um tio, por parte da mãe, têm a doença, existe o gene na família e, muito provavelmente, a mãe de Maria é portadora do gene. Logo Maria tem 50% de probabilidade de ter herdado esse gene.

Maria tem dois filhos sem a doença. Veja abaixo o heredograma de Maria. Você saberia aplicar o teorema de Bayes? Vamos usar este exemplo para ilustrar o uso do teorema de Bayes em Genética.

1.      A probabilidade de Maria ser portadora do gene para a distrofia muscular de Duchenne é ½.

2.    A probabilidade de uma portadora do gene ter dois filhos (homens) sem a doença é

3.    A probabilidade de uma não portadora do gene ter dois filhos (homens) sem a doença é 1.

4.    A probabilidade de Maria ser portadora e ter dois filhos homens sem a doença é

5.   A probabilidade Maria ser não portadora e ter dois filhos homens sem a doença é

6.   A probabilidade de a mulher ser portadora dado que tem dois filhos (homens) sem a doença é, aplicando o teorema de Bayes:

      Veja o esquema abaixo. Maria tem 20% de probabilidade de ser portadora do gene em questão.

NOTA: A doença pode ocorrer em famílias sem histórias conhecida. Veja, por exemplo, sobre distrofia muscular do tipo Duchenne:

1. Learning About Duchenne Muscular Dystrophy. https://www.genome.gov/19518854

2.   Distrofias Musculares tipo Duchenne (DMD) e tipo Becker genoma.ib.usp.br/.../distrofias-musculares-tipo-duchenne-dmd-e-tipo-be...

3. .    Sex Linkage - Learn Genetics - University of Utah. http://learn.genetics.utah.edu/content/pigeons/sexlinkage/

O exemplo citado é de

Motulsky, H. Intuitive Biostatistics. New York. Oxford University Press. 1995, p: 149-150.