Progressão geométrica ou função exponencial?

Progressão geométrica

Escolhendo Modelos de Regressão: Da Análise Exploratória à Transformação de Variáveis

Antes de ajustar uma regressão a um conjunto de pares de dados, é essencial investigar o conhecimento disponível na literatura sobre o fenômeno estudado. Verifique se existe uma teoria que explique como a variável dependente (Y) varia em função da variável independente (X). Além disso, é fundamental visualizar os dados através de um diagrama de dispersão e realizar uma inspeção numérica criteriosa.

Se houver uma teoria que relacione X e Y, avalie se os dados aderem a essa teoria. Se isso não acontecer, investigue possíveis causas. Se não houver uma teoria estabelecida, vários modelos podem ser ajustados e comparados com base em estatísticas como o coeficiente de determinação (R²), selecionando aquele que melhor representa os dados.

A Tabela 1 apresenta um conjunto de valores para as variáveis X e Y. O diagrama de dispersão correspondente (Figura 1) mostra que os pontos estão distribuídos ao longo de uma curva.

                Tabela 1. Valores de duas variáveis X e Y

                          Figura 1. Diagrama de dispersão

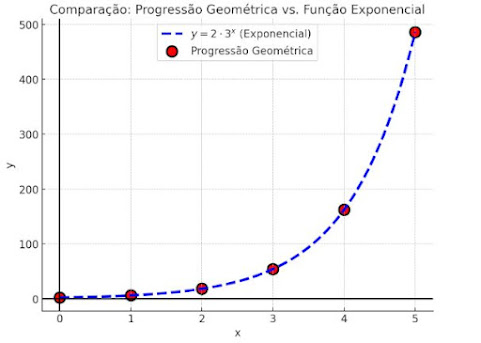
Se utilizarmos o Excel para ajustar uma reta aos dados, perceberemos que o ajuste não é satisfatório. O próprio Excel oferece outras opções de curvas que podem representar melhor a relação entre X e Y. Um ajuste exponencial pode ser uma alternativa mais adequada. Vamos comparar os coeficientes de determinação (R²) para avaliar o melhor modelo.

                         Figura 2. Ajuste exponencial dos dados

A análise mostra que a função exponencial se ajusta melhor aos dados do que a equação linear. Dessa forma, podemos expressar o modelo ajustado como:

                                      Y = 0,921e^1,273x

Quando os pontos do diagrama de dispersão não estão alinhados a uma reta, pode-se recorrer à transformação de variáveis para linearizar a função. Um método clássico é transformar a variável dependente, analisando a variação do logaritmo natural de Y em função de X.

A especificação de um modelo log-linear é comum:

                                           Y = ae^bx

Para os dados da Tabela 1, os valores de X e os logaritmos naturais de Y são apresentados na Tabela 2 e na Figura 3. O diagrama de dispersão (Figura 3) evidencia uma distribuição próxima a uma reta.

Tabela 2. Valores de X e logaritmos naturais de Y

Vamos ajustar uma regressão linear de lnY contra X. Para calcular os coeficientes de regressão a e b, usamos os logaritmos naturais de Y em vez dos valores coletados de Y. Veja na Figura 2. Se você quiser voltar ao valor da variável Y, é preciso calcular o antilogaritmo da equação.

 

                Figura 3.  Diagrama de dispersão de lnY contra X

 

Se você quiser voltar ao valor da variável Y, é preciso calcular o antilogaritmo da equação obtida. O programa Excel faz isso para você. Mas veja neste blog a postagem “Função exponencial: entenda o ajuste”.  

                           Figura 4. Ajuste de regressão não linear

As transformações são, em geral, empíricas, ou seja, dados n pares de valores X e Y, é preciso fazer várias tentativas até achar a transformação que permita ajustar uma regressão linear aos pares de dados. Outras vezes, porém, o modelo é especificado teoricamente. Procure sempre referência na literatura da área, antes de se aventurar pelos softwares.