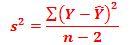Regressão linear simples

Y = a + b X + e

Regressão linear simples é um método estatístico que permite estudar a relação entre duas variáveis quantitativas, que chamaremos de X e Y.

X é a variável explicativa ou independente.

Y é a variável resposta ou dependente.

A regressão linear simples recebe o nome de “simples” porque trabalha como uma só variável explicativa. Quando a variável resposta é função de duas ou mais variáveis explicativas, a regressão linear é múltipla.

                                                             EXEMPLOS

1.    Dados peso e altura de pessoas adultas, você pode pensar em uma regressão linear simples que coloque peso como função da variável  altura. Então peso é a variável dependente e altura a variável independente.

2.    Dados peso e altura de pessoas com 6 a 10 anos de idade, você pode pensar em uma regressão linear múltipla que coloque peso com variável resposta (ou dependente) de duas variáveis explicativas (ou independente): idade e altura.Em outras palavras, o peso de uma criança depende da idade e da altura.

     RELAÇÕES DETERMINÍSTICAS E RELAÇÕES PROBABILÍSTICAS

   Antes de continuar, é preciso lembrar que duas variáveis, X e Y, podem ter uma relação determinística, ou seja, matemática, como é a relação entre graus Fahrenheit e graus Celsius:

Quando colocados em diagrama de dispersão, os pontos caem exatamente sobre uma reta, como mostra a Figura 1. Isto acontece porque a equação da reta é a descrição exata da relação entre as duas variáveis.

Figura 1

Diagrama de dispersão: pontos sobre uma reta

   Vamos estudar aqui a relação estatística entre uma variável resposta Y e uma variável explicativa X. Para começo de conversa, imagine que o fenômeno que você está estudando é bem descrito por uma reta porque, quando coloca os dados empíricos em um diagrama de dispersão, os pontos formam uma “nuvem” em torno de uma reta. Mas nessa “nuvem” caberia uma infinidade de retas. Veja a Figura 2, em que X poderia ser, por exemplo, a altura de pessoas e Y seria o peso. É preciso traçar, então, a reta que melhor se ajusta aos dados. A questão é: qual é a melhor reta?

Figura 2

Diagrama de dispersão: pontos em torno de uma reta

     É preciso estabelecer um critério para determinar a melhor reta, mas qualquer que seja a reta será sempre apenas uma aproximação para o verdadeiro fenômeno: não há como fazer previsões exatas com base em dados empíricos. E temos que nos haver com a questão estatística de estimação dos parâmetros porque a reta será ajustada usando os dados de uma amostra e não de toda a população. Quais são esses parâmetros, quando se fala em uma reta?

       A equação de uma reta é dada por

Y = a + b X,

     Nessa equação, a é o intercepto porque é o valor que Y assume quando X = 0, ou seja, quando a reta corta (intercepta) o eixo das ordenadas; b é uma medida da inclinação da reta. Não é preciso saber mais do que isto para entender a equação de uma reta, mas não custa lembrar você de que b  é a tangente trigonométrica do ângulo q  delimitado pela reta de equação Y = a + bX e pela reta paralela ao eixo das abscissas que passa pelo ponto a. Veja a Figura 3.

     Quando Y é uma variável aleatória, você pode descrever Y em função de X com o modelo:

                                              Y = a + b X + e

    Nesse modelo,  a e b são parâmetros e e é o erro aleatório. Para entender o que é o erro aleatório, observe a Figura 3: e é a distância entre a resposta de uma observação e a reta de regressão para toda a população.

Figura 3

O erro aleatório

    Se você tem dados de uma amostra, pode obter os valores a e b que estimam os parâmetros a e b da reta. Mas, para isso, é necessário fazer algumas pressuposições.

                           PRESSUPOSIÇÕES BÁSICAS

  Pressuposição 1: A relação entre as duas variáveis é linear.

Você só deve traçar uma reta para descrever um fenômeno se, no intervalo estudado, a relação entre as duas variáveis é expressa por uma reta. Para saber se a reta é, de fato, o modelo adequado para  descrever o fenômeno, existem dois procedimentos: ou você conhece a teoria que diz que o fenômeno é linear ou você “vê que a relação é  linear”, olhando o gráfico.

Pressuposição 2: A variabilidade de Y, para qualquer valor dado de X, é sempre a mesma.

A variabilidade é medida pela variância. Então esta pressuposição estabelece que a variância de Y é constante, qualquer que seja o valor de X. 

Pressuposição 3: O erro de uma observação não está correlacionado com o erro de outra observação.

As observações devem ser independentes. O que isto significa? Por exemplo, fazer a mesma pergunta 20 vezes para uma única pessoa não é igual a fazer a mesma pergunta para 20 pessoas diferentes. No primeiro caso, as respostas não são independentes: uma pessoa responde da mesma maneira (ou de maneira similar) a perguntas iguais. No segundo caso, é razoável supor que as respostas sejam independentes, desde que as pessoas tenham sido retiradas ao acaso da mesma população ( e não de um grupo fechado).

Pressuposição 4: Para qualquer valor de X, os valores de Y têm distribuição normal.

Para qualquer valor de X, os valores de Y têm distribuição normal ou, o que é o mesmo, os desvios (Y – Ŷ) têm distribuição normal. Mas esta pressuposição  só é essencial para proceder aos testes estatísticos. Os programas estatísticos geralmente fazem uma análise dos resíduos. Algumas dessas análises são gráficas e constituem a maneira fácil de visualizar se os desvios fogem muito da pressuposição de normalidade.

Pressuposição 5: Os valores de X são fixos, isto é, X não é variável aleatória.

Cabe, aqui, um comentário: essa pressuposição não é, na realidade, essencial. Em certas condições, mesmo que X seja uma variável aleatória, pode ser ajustada uma reta aos pares de valores X e Y.

Estimativas dos parâmetros

    Para obter a e b, você aplica as fórmulas dadas em seguida ou, melhor ainda, faz os cálculos usando um computador. A dedução dessas fórmulas será apresentada em nova postagem. As fórmulas são:

EXEMPLO

Este exemplo é do tutorial do SPSS: 

Uma empresa quer saber se é possível medir o desempenho no trabalho a partir de escores de QI. A empresa então faz medidas desempenho no trabalho e QI em 10 funcionários. Veja os dados apresentados na Tabela 1.

Tabela 1

Dados de QI e desempenho de dez funcionários

Para obter os valores de a e b, os cálculos intermediários estão apresentados na Tabela 2.

Tabela 2

Cálculos intermediários para obtenção de a e b

Para obter o valor de b, é preciso calcular:

    Para obter o valor de a, é preciso calcular as médias de X e de Y:

    Então:

    Obtidos os valores de a e b, pode-se escrever a equação da reta:

    Agora, é fácil traçar a reta no gráfico. Basta dar dois valores quaisquer para X (como zero e 5) e calcular os valores de Y. Para X = 0, tem-se que:

    Para X=5:

    De posse de dois pares de valores de X e Y, é possível construir o gráfico apresentado na Figura 4.

Figura 4

 Reta de regressão 

Variâncias dos parâmetros

    Para obter V(b) e V(a), você aplica as fórmulas dadas em seguida ou, melhor ainda, faz os cálculos usando um computador. As fórmulas, lembrando que s² é um parâmetro, são:

    A questão é obter uma estimativa de s². Sem aplicar uma análise de variância, que veremos em nova postagem, você calcula, para o exemplo que estamos desenvolvendo, a estimativa de s²:

    A Tabela 3 apresenta os cálculos intermediários para obter s². Lembre-se de que os valores estimados da reta são dados por

Tabela 3

Cálculos intermediários para obtenção de s²

    Você obtém o erro padrão de a e de b extraindo a raiz quadrada das respectivas variâncias. Para o exemplo:

     Para testar as hipóteses de que os parâmetros a e b são iguais a zero, contra as alternativas de que são diferentes de zero, aplique o teste t ao nível de significância desejado:

    Compare os valores calculados de t com os valores da distribuição de t com n-2 graus de liberdade e ao nível de significância estabelecido.

Para o exemplo que estamos desenvolvendo:

    No nível de 5% de significância e com n-2=8 graus de liberdade, t = 2,306. Logo, a hipótese de que b = 0 deve ser rejeitada.

    Você pode, também, obter os intervalos de confiança para os parâmetros a e b. Sendo t₀ o valor crítico de t com n-2 graus de liberdade e ao nível escolhido de significância, você ontem os intervalos como segue: 

        Para o exemplo:

Se você usar o SPSS, vai obter, para o que foi visto aqui:

                       VEJA REGRESSÃO LINEAR PASSANDO PELA ORIGEM EM OUTRA POSTAGEM.

Kolmogorov- Smirnov : teste de normalidade

Aplicamos o teste de aderência de Kolmogorov-Smirnov para verificar se determinada amostra provém de uma população com distribuição específica. Essa “distribuição específica” é, na maioria das vezes, a distribuição normal. Nesses casos, podemos dizer que estamos usando o teste de normalidade de Kolmogorov-Smirnov.

Vamos ver, por meio de um exemplo, o procedimento para testar a hipótese de que os erros em torno da média seguem uma distribuição normal, utilizando o teste de normalidade de Kolmogorov-Smirnov.

EXEMPLO

Com um cronômetro na mão para medir o período de oscilação de um pêndulo, você realiza n = 20 medições. Os resultados estão apresentados na Tabela 1. 

A média aritmética das n=20 medidas é a melhor estimativa para o período de oscilação:

Tabela 1
Leituras do período de oscilação de um pêndulo, em segundos 

              A média aritmética das n=20 medidas é a melhor estimativa para o                                  período de oscilação:

             Os desvios em relação à média estimamos erros de medição. Veja a                                  Tabela  2. 

 Tabela 2

Desvios da média das leituras do período
de oscilação de um pêndulo, em segundos 

A média dos desvios é: 

                            

Como essa média é igual a zero, o desvio padrão é dado por: 

Podemos organizar os dados em uma tabela de distribuição de frequências (Tabela 3) e desenhar o histograma correspondente, apresentado na Figura 1.

Tabela 3
Tabela de distribuição de frequências

 Figura 1

Histograma dos desvios da média das leituras do período
de oscilação de um pêndulo, em segundos

 

Podemos sobrepor ao histograma uma curva normal com a mesma média e desvio padrão dos desvios apresentados na Tabela 2. Veja a Figura 2.

Figura 2
Distribuição normal sobreposta ao histograma

 

Para aplicar o teste de Kolmogorov-Smirnov:

1.    Calcule as frequências acumuladas (FAᵢ) dos desvios.

2.   Calcule as frequências relativas acumuladas (FRAᵢ) dos desvios.

3.   Calcule o valor padronizado (ou estandardizado) zᵢ para cada desvio dᵢ ​. A média será sempre zero, mas para o exemplo em questão, o desvio padrão calculado é s = 0,1487s. Então, neste caso:

                         

4.     Determine as probabilidades acumuladas Pᵢ dos desvios padronizados sob a distribuição normal padronizada. Veja a Figura 3, em que a probabilidade acumulada até z = −1  está destacada em cinza azulado. 

Figura 3
Probabilidade acumulada sob a distribuição normal padronizada

 

5.   Calcule os valores absolutos das diferenças Dᵢ entre as frequências relativas acumuladas dos desvios (FRAᵢ) e as probabilidades acumuladas (Pᵢ).

6.   Calcule os valores absolutos das diferenças Dᵢ’ entre as probabilidades acumuladas (Pᵢ) e as frequências relativas acumuladas da classe imediatamente anterior (FRAᵢ₋₁).

7.   Compare o maior valor observado entre Dᵢ e Dᵢ’ com o valor crítico D obtido na tabela de valores críticos do teste de Kolmogorov-Smirnov para dados contínuos. A estatística de teste é:

8.   Rejeite a hipótese H0 de que os desvios seguem distribuição normal se a estatística D calculada for maior que o valor crítico correspondente ao nível de significância estabelecido e ao tamanho da amostra. Veja os resultados desses cálculos na Tabela 4.                            

                                                      Tabela 4

              Cálculos auxiliares para o teste de aderência de Kolmogorov-Smirnov 

O valor máximo encontrado para D foi 0,150, menor que o valor crítico para o nível de significância de 5% e tamanho amostral 20. Portanto, não se rejeita a hipótese de que a distribuição dos desvios é normal.

Valores críticos para D para o teste de aderência de

Kolmogorov-Smirnov para variáveis contínuas

       Fonte: ZAR,J. Biostatistical Analysis. 4 ed. Prentice Hall. 1995.

                                  Comentário Adicional

É bastante comum, quando se pretende aplicar uma análise de variância (ANOVA) aos dados experimentalmente, que se faça a pressuposição de que os erros são variáveis aleatórias independentes com distribuição normal. Veja um exemplo.

EXEMPLO

 

Todo produtor de milho quer ter maior produtividade. Imagine que um produtor colocou à disposição de um agrônomo uma pequena área onde foi possível alocar 20 parcelas para a experimentação de três híbridos além do que chamaremos testemunha, ou seja, o que o produtor planta em sua propriedade. A Tabela 6 apresenta os dados segundo o tratamento e, no rodapé, as médias. Até que ponto as diferenças observadas entre as médias dos tratamentos são suficientemente grandes para serem tomadas como evidência de que há diferença significante entre eles? A resposta para essa pergunta é dada por uma análise de variância, que testa a hipótese de que as médias populacionais são iguais, isto é:

contra a hipótese alternativa de que existe pelo menos uma média diferente das demais. 

                                                         Tabela 5

 Produtividade de milho segundo o tratamento

Outros testes de normalidade

Há vários testes de aderência à distribuição normal. Alguns deles, como o de Anderson-Darling e o de Cramer-von Mises (1) são, na realidade, melhoramentos feitos sobre o teste de Kolmogorov- Smirnov[1]. Como são mais poderosos, são preferidos por muitos analistas.

Vamos apresentar aqui (só para exemplo) o que se faz comumente na prática de estatística. São os testes de Shapiro-Wilk e um plot. Normalmente o Q-Q plot.

Resultado do teste de Shapiro-Wilk

·     Estatística W: 0.9396

·     Valor-p: 0.2359

·     Média dos resíduos: 0.0000

·     Desvio padrão dos resíduos: 2.4279

Com p-valor = 0.2359 (> 0.05), não rejeitamos a hipótese da nulidade: os resíduos seguem uma distribuição normal. 

O teste de Shapiro-Wilk, proposto em 1965, tem se saído muito bem nos estudos de comparação com outros testes de aderência. Usa uma estatística complicada, que não será dada aqui. Para bem entender a estatística de teste, veja o trabalho original[2]. Mas é comum nos programas de computador e deve ser preferido quando a amostra é pequena.

                                      Q-Q Plot dos Resíduos (Desvios) 

Q-Q plot dos resíduos (desvios): os pontos seguem bem a linha vermelha, o que confirma a normalidade dos resíduos observada no teste de Shapiro-Wilk.

Figura 4

Q-Q Plot dos Resíduos (Desvios)

 

                     [1] Kolmogorov-Smirnov Goodness-of-Fit Test. https://www.itl.nist.gov/div898/handbook/eda/.../eda35g.htm

                          [2]The Shapiro-Wilk and related tests for normality. https://math.mit.edu/~rmd/465/shapiro.pdf

---