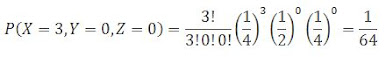Suponha que, em uma população
parental de moscas das frutas, a
frequência de alelos para o fracasso (F) de um inseticida usado no combate das
moscas seja ½ e a frequência de alelos para sucesso (S) seja ½.
Frequência
de alelos para fracasso (F) = ½.
Frequência
de alelos para sucesso (S) = ½.
A
frequência de gametas F e S na população é a mesma, ou seja:
Frequência de gametas para fracasso (F) = ½.
Frequência de gametas para sucesso (S) = ½.
No caso
de organismos diploides, os gametas têm distribuição binomial, uma vez que são possíveis apenas ou S ou F. Lembre-se
de que
Vamos
supor que apenas três zigotos sobreviveram quando o inseticida foi aplicado.
Uma
amostra dos zigotos resulta em um processo trinomial,
porque há três genótipos possíveis: FF, FS e SS. Seja X o número de zigotos FF, Y
o número de zigotos FS e Z o número
de zigotos SS.
A probabilidade de ocorrerem x
zigotos FF, y zigotos FS e z zigotos SS é dado por:
1ª pergunta: Qual
é a probabilidade de os três zigotos serem homozigotos?
2ª pergunta: Qual
é a probabilidade de cada zigoto ter um tipo de genótipo?
3ª pergunta: Qual
é a probabilidade de que os três zigotos sejam FS?
Lembrando combinações:
Imagine
uma sequência de n eventos (ou
n ensaios, ou n tentativas) idênticos e independentes. São três os resultados
possíveis para cada evento: “A”, “B” e “C”.
Se a
probabilidade de A (ocorrer o evento de interesse) for p, a
probabilidade de B for q e a probabilidade de C for 1-p-q,
você tem uma distribuição
trinomial.
Imagine agora uma sequência de n
eventos:
A,
A,...,A ocorre x vezes;
B, B,...,B
ocorre y vezes;
C, C,...,C
ocorre z vezes.
De quantas maneiras isso pode acontecer? Como
x + y + z = n, z = n -
x - y: