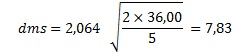Além do F: comparações certeiras com o teste de Scheffé

Feita a análise de variância, se o valor do teste F for significante — ou seja, se rejeitarmos a hipótese de que todas as médias são iguais —, é possível aplicar o teste de Scheffé para comparar contrastes de médias. Antes, porém, é fundamental entender o que é um contraste.

O que é um contraste de médias?

De maneira simples, um contraste de médias é uma combinação linear de médias de grupos, em que a soma algébrica dos coeficientes é igual a zero.

Por exemplo, suponha que o pesquisador deseje comparar três médias de grupos. A s expressão:

                     

é um contraste de médias porque:

                 ·        É uma função linear de médias;

                  ·        A soma dos coeficientes é 1+1−2 = 0.

Substituindo os parâmetros (μi) pelas respectivas estimativas, obtemos a estimativa do contraste de médias:

                    

E a variância do contraste?

Em uma análise de variância, a variância dos resíduos é estimada pelo quadrado médio do resíduo (QMR). Se os grupos têm o mesmo número de repetições (r), a variância da estimativa do contraste é dada por:                                                                                              

  Como aplicar o teste de Scheffé?

Para verificar se um contraste de médias é estatisticamente significante a um dado nível , o teste de Scheffé utiliza a seguinte expressão crítica:

Onde:

                        ·        k é o número de grupos;

                 ·    F_crítico é o valor da tabela F, com k−1 graus de liberdade no numerador e os graus de liberdade do resíduo​ no denominador;

                      ·        Var(L) é a variância estimada do contraste.

Se o valor absoluto do contraste L for maior que S, o contraste é considerado estatisticamente significante.

Exemplo Aplicado

Considere os dados da Tabela 1, analisados por ANOVA (Tabela 2). O valor de F é significante no nível de 5%, indicando que pelo menos uma média difere das demais. As médias dos grupos estão na Tabela 3.

Tabela 1. Dados observados, segundo o grupo

                        

Tabela 2. Análise de variância

Tabela 3. Médias segundo o grupo

Vamos testar a hipótese de que as respostas dos grupos tratados são, em média, maiores que a do grupo controle, utilizando o teste de Scheffé.

1.     Cálculo do contraste de médias

2.     Cálculo da variância do contraste

3.     Valor crítico de F

Com 5 graus de liberdade para grupos e 24 graus de liberdade no resíduo é 2,62.

Valor crítico de Scheffé

Como o valor absoluto do contraste calculado  L = 71 é maior que o valor crítico S, concluímos que os grupos tratados apresentam, em média, respostas significativamente maiores que o grupo controle.

 

Teste da DMS de Fisher para comparação de médias

Se a análise de variância (ANOVA) indicar um valor de F significativo, o pesquisador precisa recorrer a um teste post hoc, com o objetivo de identificar quais médias diferem entre si. Existem vários testes desse tipo, geralmente nomeados a partir de seus autores. O mais antigo deles é o teste LSD (Least Significant Difference), proposto por Fisher, conhecido em português como DMS — Diferença Mínima Significante.

                Como aplicar o teste DMS de Fisher

Para aplicar o teste, siga estes passos:

1.       Calcule as médias dos grupos.

2.       Estabeleça o nível de significância desejado.

3.       Calcule a DMS utilizando a fórmula:

em que:

·     t é o valor da distribuição t de Student, associado ao nível de significância escolhido e aos graus de liberdade do quadrado médio do resíduo (QMR) da ANOVA;

·     QMR é o quadrado médio do resíduo, obtido na tabela da ANOVA;

·       r é o número de repetições em cada grupo.

Exemplo

Considere um ensaio clínico para avaliar o efeito de cinco drogas na redução da pressão arterial. Participaram 30 pacientes, divididos aleatoriamente em seis grupos de cinco participantes cada. Um grupo recebeu placebo, enquanto os demais receberam as cinco drogas em teste.

A Tabela 1 mostra a redução da pressão arterial durante o ensaio (diferença entre os valores inicial e final). Os dados foram analisados por ANOVA, com os resultados apresentados na Tabela 2.

            Tabela 1 – Redução da pressão arterial segundo o tratamento

 Tabela 2 – Análise de variância (ANOVA)

Como o valor de F foi significativo, podemos aplicar o teste DMS de Fisher. Temos que:

·      Nível de significância: 5%

·      Graus de liberdade do resíduo: 24

·      Valor t: 2,064

·      QMR (quadrado médio do resíduo): 36,00

·      Repetições por grupo: r = 5

Calculamos:

Toda diferença entre médias maior ou igual a 7,83 é considerada estatisticamente significativa.

As comparações, par a par, (pairwise comparisons) são apresentadas na Tabela 3 e na Figura 1.

           Tabela 3 – Comparações entre médias pelo teste DMS de Fisher

Médias que não compartilham letra são significativamente

diferentes.

              Figura 1 – Comparações entre médias pelo teste DMS de Fisher

Teste das amplitudes múltiplas de Duncan (Duncan's multiple range test)

Uma análise de variância (ANOVA) pode indicar se existe diferença significante entre grupos, mas não informa quais grupos diferem entre si. A ANOVA é, portanto, um teste global. Para identificar as diferenças específicas, é necessário comparar as médias logo após o teste global.

Métodos usados para comparar médias depois de uma ANOVA são chamados testes a posteriori ou post hoc comparisons. Entre os testes mais conhecidos — e amplamente disponíveis em pacotes de estatística — estão o teste de Tukey (já tratado em postagem anterior) e o teste de Duncan, que abordaremos aqui.

O teste de Duncan, conhecido na literatura em língua inglesa como Duncan’s Multiple Range Test (MRT), é aplicado após uma ANOVA para identificar quais pares de médias (em experimentos com pelo menos três grupos) diferem estatisticamente. Diferentemente do teste de Tukey, ele não realiza comparações apenas duas a duas: é um teste sequencial baseado em amplitudes mínimas significantes.

Embora mais trabalhoso — exige calcular diversas amplitudes mínimas — o teste de Duncan é muito utilizado. Vamos mostrar seu funcionamento com um exemplo.

Exemplo

Considere os dados fictícios de diminuição da pressão arterial apresentados na Tabela 1. Esses dados foram submetidos à ANOVA, cujos resultados estão na Tabela 2. Como o valor de F foi significativo ao nível de 5%, podemos concluir que existe pelo menos uma média diferente das demais. As médias amostrais estão na Tabela 3.

Tabela 1 – Diminuição da pressão arterial (mmHg)

segundo o grupo

Tabela 2 – Resultado da análise de variância (ANOVA)

Tabela 3 – Médias de diminuição da pressão arterial (mmHg)

segundo o grupo

 

Pergunta: Quais médias são estatisticamente diferentes?

Para responder, aplicamos o teste de Duncan. Antes, vamos entender sua lógica.

Como Funciona o Teste de Duncan

O teste de Duncan compara a amplitude (diferença) de conjuntos de médias amostrais ordenadas com uma amplitude mínima significante calculada (Rm).

·  Se a amplitude observada excede a amplitude mínima calculada, considera-se que as médias populacionais são diferentes ao nível de significância escolhido.

·  O teste é passo a passo ou sequencial (stepwise): inicia-se pela comparação entre a maior e a menor média. Se a diferença for significativa, seguem-se as comparações entre as médias mais próximas.

Se, em algum ponto, uma diferença não for significativa, as comparações subsequentes não são realizadas.

Etapas do Teste

       1.     Ordenar as médias em ordem decrescente (ou crescente).

                 Tabela 4 – Médias ordenadas (diminuição da pressão arterial, mmHg)

        2.     Calcular a amplitude mínima significante (Rm) para cada número de médias envolvidas (m). A fórmula é

                                     

Onde:

·  r_m= valor crítico da amplitude mínima estudentizada (least significant studentized range), encontrado em tabelas específicas;

·  QMR = quadrado médio do resíduo da ANOVA;

·  r = número de repetições por grupo.

Tabela 5-Amplitude estudentizada mínima significante

no nível de significância de 5%

(Uma amostra da tabela para obter rm ) 

Aplicação ao Exemplo

·  Número de médias: k = 6

·  QMR=36,00 (Tabela 2)

·  r = 5 (Tabela 1)

·  Graus de liberdade do resíduo = 24

Consultando Harter (1960) – referência: Harter, H. L. Critical values for Duncan´s new multiple range test. Biometrics, 16(4):671–685, 1960 – obtemos os valores de rm.                     

Primeira Comparação:

·  Para m = 6, segue-se r_m = 3,276.

·  Diferença entre D e Controle: diferença = 29 – 2 = 27

·  R_m para 6 médias:

                 

· Como 27 > 8,7927, a diferença é significativa.

Comparações seguintes:

Para m = 5:

·  Comparações: D e B (diferença = 21), A e Controle (diferença = 19)

·  r₅ ≈ novo valor calculado                       

·  Ambas diferenças significativas.

Para m = 4:

            ·      Comparações: D e C (diferença = 19), A e B (diferença = 13), E e Controle (diferença = 11).

·        Todas diferenças significativas.

Para m = 3:

·        Comparações: D e E (diferença = 16), A e C (diferença = 11)

·        Ambas diferenças significativas.

·   Comparações E e B (diferença = 5) e C e Controle (diferença = 8) não são significativas.

Assim, para conjuntos não significativos, não se prossegue com comparações internas.

Para m=2

·        D e A (diferença = 8), A e E (diferença = 8)

·        Ambas diferenças significativas.

Apresentação Final dos Resultados

A apresentação usual em softwares de estatística é:

Tabela 6 – Comparação de médias pelo teste de Duncan

Nota: Médias que compartilham a mesma letra

 não diferem significativamente.

É importante notar que não podem ser testadas diferenças de médias que estão dentro de um intervalo de médias  que não são estatisticamente diferentes. É comum apresentar as médias de grupos em ordem decrescente ou crescente. As médias são sublinhadas. Médias sublinhadas por uma mesma linha não têm diferença significante. Veja o exemplo.

Observação Final

Se os grupos forem de tamanhos diferentes, substitua r pela média harmônica dos tamanhos dos grupos no cálculo de R_m.