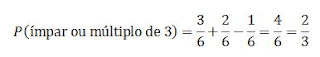Probabilidade: vamos resolver exercícios?

PARA ENGENHEIROS: qual é a variância?

                                 

    No processo de extração de ouro, o minério é separado em duas partes: concentrado e rejeito. Assim, a partir de uma quantidade M de minério, obtém-se uma quantidade C de concentrado e uma quantidade R de rejeito. Podemos expressar isso da seguinte maneira:

                                M = C + R

    São feitas determinações do teor de ouro, tanto no minério como no concentrado. É possível, a partir da variância das determinações do teor de ouro no minério e da variância das determinações do teor de ouro no concentrado, obter a variância do teor de ouro no rejeito?

    Para responder à questão, seja:

·        m o teor de ouro no minério,

·        c o teor de ouro no concentrado,

·        r o teor de ouro no rejeito.

Então, a quantidade Mm de ouro no minério é dividida em duas partes, da seguinte maneira:

                            Mm = C c + R r

    Segue-se daí que:

                     

    Como R = M – C, tem-se que 

               

    É razoável considerar que os erros de medida das quantidades M e C são desprezíveis em comparação com os erros de medida nos teores de ouro. Ao desconsiderar as variâncias de M e C e assumir que m e c são variáveis independentes, podemos calcular a variância do teor de ouro no rejeito:              

 

Riscos e estatísticos

Estatística é a ciência que fornece os princípios e a metodologia para coleta, organização e análise de dados. Por conta disso, os pesquisadores das mais diferentes áreas buscam, uma vez ou outra, um consultor (a) de estatística. Mas o consultor de estatística deve ter, além de conhecimento na área, habilidade para estabelecer bom relacionamento com os profissionais que o procuram. é um risco, de parte a parte.

   Muitos anos de atividade como consultora de estatística me convenceram de que é raro reunir, numa única entrevista, um problema interessante para o consultor, um pesquisador inteligente e disposto a estudar e uma situação favorável de trabalho. Mas quando essas três condições estão ausentes, fica difícil lidar com a situação. Um constante alerta para as questões de ética talvez seja a melhor defesa contra os reveses que podem ocorrer. E são muitos os meandros da consultoria estatística que trazem, em seu bojo, a possibilidade de frustração e sensação de derrota.

     Alguns percalços, porém, têm alto risco. Existem pesquisadores que esperam demais do consultor de estatística: querem que o consultor se entusiasme pelo trabalho deles, repita explicações várias vezes porque eles “não são bons na matemática”, tenha tempo sempre que eles precisarem e redija os resultados, além de se responsabilizar pelas conclusões. 

     Também é comum que um pesquisador apresente o trabalho feito pelo estatístico como sendo seu, sem sequer referenciar o nome do profissional que consultou. É fácil medir o risco: basta olhar algumas revistas especializadas e procurar pelos artigos que expõem análises estatísticas sofisticadas. Grande parte desses artigos não dá o nome de quem fez a análise, o nome do programa de computador utilizado ou o título de um livro didático que exponha a técnica utilizada. Quando perguntados sobre o autor das análises estatísticas, os autores alegam que o serviço de estatística foi pago – e esquecem que eles também são pagos para trabalhar.

         Não é claro, porém, quando o estatístico deva ser coautor do trabalho. Há exageros dos dois lados. Alguns estatísticos exigem coautoria de trabalhos em que somente calcularam médias e desvios padrões e desenharam gráficos. Isso é inaceitável porque, em tais casos, o trabalho do estatístico é de consultor. Outras vezes, o nome do estatístico não é sequer citado em trabalhos que exibem, por exemplo, o ajuste de uma função logística passo a passo para dados de resposta quântica, com testes e intervalos de confiança.

      Entretanto, a melhoria do status profissional do estatístico nas áreas da saúde depende tanto de o estatístico aprender a dar consultoria como de o pesquisador aprender metodologia científica. Os estatísticos começam a dar consultoria sem qualquer tipo de treinamento. No curso de Estatística, o aluno não aprende metodologia científica nem discute consultoria. Interage pouco com profissionais de outras áreas. O enfoque é a teoria. Já os profissionais das áreas da saúde tiveram aulas de Bioestatística, mas no início do curso, em salas superlotadas. O professor, que sente o desinteresse dos alunos, muitas vezes ensina apenas a usar um programa de computador e não ensina que a Estatística dá suporte à pesquisa científica. 

    De qualquer modo, a quantidade de atenção dada pelo consultor de estatística ao pesquisador depende de diversos fatores, tais como competência profissional do consultor, propostas alternativas de trabalho, conhecimento de estatística por parte do pesquisador, status profissional do pesquisador, política do ambiente de trabalho, simpatia e sentimentos pessoais. A ideia de que a interação pessoal não ocorre em ciência e que o consultor é um indivíduo calmo e reservado não confere com a realidade. A consultoria estatística é um caos: trabalha-se sob a pressão de tempo, da falta de verba, da política do ambiente de trabalho e da discriminação profissional. Da discriminação profissional sim – porque há pesquisadores que ainda pensam que o estatístico é mero acessório de computador.

 

 

Teorema da soma de probabilidades ou a regra do ou

Para bem entender o teorema da soma de probabilidades, ajuda dividir a questão em duas regras:

·   regra nº 1, para soma de eventos mutuamente exclusivos;

· regra nº 2, para soma de eventos não mutuamente exclusivos.

                       Eventos mutuamente exclusivos

Dois eventos são mutuamente exclusivos quando não podem ocorrer ao mesmo tempo.

 Exemplo

Quando um dado é lançado, só pode ocorrer uma das faces. Se a ocorreu a face “cinco”, ficou excluída a possibilidade de ter ocorrido qualquer outra face.

Regra 1 da soma

(para eventos mutuamente exclusivos)

 

Se A e B são eventos mutuamente exclusivos, a probabilidade de ocorrer A ou B é igual à soma das probabilidades de ocorrer cada um deles. Escreve-se:

                         

 Exemplo

 Quando você joga um dado, só pode ocorrer uma das faces. Qual é a probabilidade de, em um lançamento, ocorrer 1 ou 6? Usando a regra 1 da soma, você calcula a probabilidade de ocorrer 1 e a probabilidade de ocorrer 6. Depois, soma essas probabilidades.

                       

                                             Exemplo

Imagine um pote de vidro com 11 bolinhas de diferentes cores: 3 azuis, 4 brancas, 2 vermelhas, 1 amarela, 1 verde. Qual é a probabilidade de, em uma só retirada, ocorrer bola verde ou bola amarela? Usando a regra 1 da soma, você calcula a probabilidade de ocorrer bola verde e a probabilidade de ocorrer bola amarela. Depois, soma essas probabilidades.

  Eventos não mutuamente exclusivos

Dois eventos A e B são não mutuamente exclusivos se eles têm pelo menos um resultado em comum.

Exemplo

Quando você joga um dado, só pode ocorrer uma das faces. Mas pense nos eventos: ocorrer “número ímpar” ou ocorrer “número maior do que quatro”. Esses dois eventos têm um resultado em comum: é o número cinco, que tanto pertence ao evento “número ímpar” como ao evento “número maior do que quatro”.

Veja a figura: “números ímpares” estão circundados por uma elipse azul e “números maiores do que quatro” por um retângulo vermelho. Se você contar o número de resultados que correspondem ao evento “número ímpar” e o número de resultados que correspondem ao evento “número maior do que quatro”, terá contado 5 duas vezes.  

                   

Regra 2 da soma

(para eventos não mutuamente exclusivos)

Se A e B são dois eventos não mutuamente exclusivos, há uma sobreposição, isto é, existe pelo menos um resultado de A que também é resultado de B. Então a probabilidade de ocorrer A ou B é dada pela probabilidade de A, mais a probabilidade de B, menos a probabilidade de A e B (que foi contada duas vezes). Escreve-se:

             

Exemplo

Quando você joga um dado, só pode ocorrer uma das seis faces. Qual é a probabilidade de, em um lançamento, ocorrer “número ímpar” ou ocorrer “número maior do que quatro”? Usando a regra 2 da soma,  calcule a probabilidade de ocorrer “número ímpar”, a probabilidade de ocorrer “número maior que quatro” e probabilidade de ocorrer “número ímpar maior do que quatro”. Depois, aplique a regra

Exemplo

Uma carta será retirada ao acaso de um baralho. Qual é a probabilidade de sair um rei ou uma carta de copas?

Como um baralho tem 52 cartas, das quais quatro são reis e 13 são de copas, alguém poderia pensar que a probabilidade de sair um rei ou uma carta de copas é dada pela soma das probabilidades de sair um rei e de sair uma carta de espadas. Mas esta resposta está errada porque o rei de copas é tanto rei como copas. Então o rei de copas teria sido contado duas vezes – como rei e como copas.                                                  

            

Exercícios

1. É dado o conjunto de dados: A={1; 2; 3; 4; 5; 6; 7; 8; 9; 10}.

     a) Qual é a probabilidade de, ao se tomar um número ao acaso desse conjunto A de dados, o número ser um ímpar menor do que 4 ou um ímpar maior do que 8?
    b)    Qual é a probabilidade de, ao se tomar um número ao acaso desse conjunto A de dados, o número ser um ímpar ou múltiplo de 3?

           2. Qual é a probabilidade de, ao lançar um dado, sair número ímpar ou múltiplo de 3? 

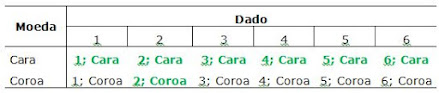
            3. Jogam-se um dado e uma moeda. O jogador ganha se sair “cara” na moeda ou “2” no dado. Qual é a probabilidade de o jogador ganhar arremessando juntos o dado e a moeda?

                                         Respostas

     1.  a) 3/10.

     1.  b) 3/5.
                 2.  2/3
                 3. 7/12

 

                       Como se chega a essas respostas?

1.a) São 10 eventos possíveis. São eventos de interesse: ímpares menores do que 4, isto é, 1 e 3 e maiores do que 8, ou seja, só o 9. Veja os eventos de interesse em vermelho:
                     1; 2; 3; 4; 5; 6; 7; 8; 9; 10. 
Daí, a resposta 3/10.
1.b) São 10 eventos possíveis. São eventos de interesse: ímpares ou múltiplos de 3. São ímpares: 1; 3; 5; 7; 9. São múltiplos de 3: 3; 6; 9. Veja que os números 3 e 9 foram contados duas vezes, porque são tanto números ímpares como múltiplos de 3. Usando a regra 2 da soma:

Veja as respostas de interesse marcadas em vermelho (ímpares) e circundadas por quadrado (múltiplos de 3):

               

2. São 6 eventos possíveis, dos quais 3 são números ímpares e 2 são múltiplos de 3, mas 3 é tanto ímpar como múltiplo de 3. Então, aplicando a regra 2 da soma:

Marcadas em vermelho, múltiplos de 3 e, em azul, os ímpares.
                  

       

3. Veja: tanto faz sair “cara” na moeda ou “2” no dado, o jogador ganha nos dois casos. A probabilidade de sair “cara” na moeda é

  A probabilidade de sair “2” no dado é 

                            

No entanto, pode “sair cara” na moeda e “2” no dado em uma única jogada. A probabilidade desse evento é

 Logo, para calcular a probabilidade de o jogador ganhar, use a regra 2 da soma. A probabilidade pedida é

Veja também a tabela e conte: são 12 eventos possíveis; 7 são de interesse. Logo, a probabilidade pedida é 7/12.3. Veja: tanto faz sair “cara” na moeda ou “2” no dado, o jogador ganha nos dois casos. A probabilidade de sair “cara” na moeda é

Conjuntos

Conjuntos são coleções de itens. Você pode pensar no conjunto de pessoas que vai convidar para sua festa de aniversário, no conjunto de feriados no semestre, no conjunto de árvores de uma praça, no conjunto de roupas que vai precisar para uma viagem.

Elementos são os itens contidos no conjunto. Para designar os elementos de um conjunto, você deve escrevê-los em sequência, entre chaves e separados por vírgulas. Por exemplo, seja I o conjunto de seus irmãos. Se eles se chamam Mateus e Lavínia, o conjunto de seus irmãos é escrito da seguinte forma:

                              I = {Mateus, Lavínia}

Diagrama de Venn é uma representação gráfica na qual os elementos de um conjunto são ilustrados dentro de círculos. No diagrama, há sempre dois ou mais círculos, e cada círculo representa um conjunto.

Para desenhar um diagrama de Venn, comece traçando um retângulo, que representará o todo ou universo. Em seguida, desenhe dentro dele os círculos que representarão os conjuntos.

Por exemplo, suponha que você seja torcedor de um time de futebol que disputa um campeonato. Nesse caso, você pode considerar dois conjuntos de jogadores: os do “seu” time e os do time rival.

Conjuntos disjuntos, ou mutuamente exclusivos, são aqueles que não possuem elementos em comum. É o caso do exemplo que acabamos de ver.

 Há conjuntos que possuem elementos em comum, ou seja, um ou mais elementos pertencem simultaneamente a dois ou mais conjuntos. Por exemplo, imagine o conjunto D de animais domésticos e o conjunto F de felinos. O gato pertence aos dois conjuntos. 

 No diagrama de Venn, existe uma região onde os círculos se sobrepõem. Essa região é chamada de intersecção e representada por D∩F, que se lê D intersecção F.

 

Quando estamos interessados nos elementos de um conjunto ou de outro, dizemos que estamos interessados na união dos conjuntos. Por exemplo, se o diretor de uma escola deseja falar com alguém da comissão de formatura, formada por alunos (conjunto A) e professores (conjunto P), não importa se essa pessoa é aluno ou professor – o diretor está interessado em um elemento de A união P.

 A região correspondente à união é representada por A∪P, que se lê A união P.

 

Universo é o conjunto de todos os elementos possíveis. É geralmente indicado pela letra U. No primeiro exemplo que vimos, em que se suponha que você fosse torcedor de um time de futebol que disputa um campeonato, o universo poderia ser constituído por todos os jogadores de futebol.

Conjunto vazio é aquele que não possui nenhum elemento. Por exemplo, o conjunto de universitários analfabetos é vazio. Esse conjunto é indicado pela letra grega ∅ (lê-se fi). Podemos usar o conhecimento sobre conjunto para resolver problemas ¹.

Exemplo ²: Em um canil estão 24 cães: 12 são pretos, seis têm cauda curta e 15 têm pelos longos. Apenas um cão é preto, tem cauda curta e pelos longos. Dois cães são pretos e têm cauda curta, mas não têm pelos longos. Outros dois cães têm cauda curta e pelos longos, mas não são pretos. Se todos os cães do canil têm pelo menos uma das características citadas, quantos cães são pretos, com pelos longos, mas não têm cauda curta?

                                  Exemplo (2)
Em um canil, há 24 cães:

                             ·    12 são pretos ,

                            ·    6 têm cauda curta,

                            ·    15 têm pelos longos.

   Informações adicionais:

                  ·    Apenas 1 cão é preto, tem cauda curta e pelos longos.

                  ·    2 cães são pretos e têm cauda curta;  não têm pelos longos.

                   ·    2 cães têm cauda curta e pelos longos, mas não são pretos.

   Pergunta:

Quantos cães são pretos, têm pelos longos, mas não têm cauda curta?

·  O número de cães em cada categoria está escrito no respectivo círculo, com realce em amarelo.

·       O número de cães em cada interseção está em vermelho.

·     Pergunta-se o número (incógnita) de cães na interseção dos três círculos.

               

 

·       Usando os dados que estão ao lado dos círculos (com realce amarelo), faça as contas para determinar quantos cães estão em cada um dos conjuntos: pretos, cauda curta, pelos longos. Esses cálculos estão indicados em letras azuis.

·       Somando os números de cães em cada um dos conjuntos, você obtém o número de cães no canil:

9-x+2+1+x+1+2+12-x =24

·       Para achar x:

                                                        -x+x-x+9+2+1+1+2+12

                                                       27- x=24

             x=3

Três cães são pretos, têm pelos longos, mas não têm cauda curta

 Referências

1.    Working with Sets and Venn Diagrams. http://www.regentsprep.org/regents/math/algebra/ap2/lvenn.htm

2.    Elementary Test Prep: Math 4 Test (Grades 4) Draw a Picture

www.studyzone.org/testprep/math4/.../drawpict4l.cf..