Quando se comparam k populações por meio de uma ANOVA, são possíveis m = k(k-1)/2 comparações entre pares de médias. Se essas comparações não foram planejadas previamente (unplanned comparisons), ou seja, foram escolhidas depois de o pesquisador olhar as médias amostrais, é mais adequado utilizar um teste que controle o nível de significância para o experimento e não apenas o nível de significância para a comparação de médias.
Definições Importantes
🔸Nível de significância para comparação de médias (comparisonwise Type I error rate-CER) é a probabilidade de cometer erro Tipo I ao comparar duas médias (pairwise comparison) de um conjunto de k médias.
🔸Nível de significância para experimentos (experimentwise Type I error rate ou familywise Type I error rate) é a probabilidade de cometer pelo menos um erro Tipo I ao realizar todas as m comparações de pares de médias de um conjunto de k médias.
Distinguem-se
ainda:
🔸Nível de
significância para o experimento sob a hipótese de nulidade completa (EERC):
quando todas as médias populacionais comparadas são iguais.
🔸Nível de significância para o experimento sob a
hipótese de nulidade parcial: quando algumas médias são iguais, outras diferem.
Testes que controlam o nível de
significância para experimentos são conservadores —rejeitam
a hipótese de igualdade de médias com menos facilidade, resultando em menor
poder estatístico. Já os testes que controlam o nível de significância para
comparações de médias apontam significância com mais facilidade. Estes testes
são liberais, porque rejeitam a hipótese da nulidade com mais
facilidade e têm, portanto, maior poder.
Classificação
dos Testes: Liberal x Conservador
Segundo Winner (1962), os testes de comparação de
médias podem ser ordenados do mais liberal ao mais conservador, como
segue:
1.
Teste de Duncan (Duncan´s multiple range test -MRT)
2. Teste de Student-Newman-Keuls
3. Teste de Fisher (Fisher’s least
significant difference- LSD)
4. Teste de Tukey (Tukey’s honestly
significant difference- HSD)
5.
Teste de
Scheffé (Scheffé’s test)
Isso significa que, se você aplicar o teste de
Duncan, provavelmente encontrará mais diferenças significantes entre médias do
que se utilizar o teste de Scheffé. Mas há vários outros testes para comparação
de médias.
Apresentamos a seguir os resultados de testes de
comparação de médias aplicados a um conjunto de dados fictícios.
Tabela 1
Diminuição da pressão arterial, mmHg,
segundo o grupo
Análise de variância
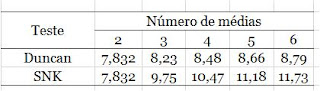
O teste de amplitudes múltiplas de Duncan (Duncan’s multiple range test-MRT) e o teste de Student-Newman-Keuls fornecem diversos valores para a diferença crítica entre médias, dependendo de quão próximas estão essas médias. Compare as amplitudes críticas: o teste de Duncan é mais liberal, ou seja, mostra significância com maior facilidade (note que as diferenças mínimas significantes são menores pelo teste de Duncan).
Tabela 3
Amplitude crítica: testes de
Duncan e
Student-Newman-Keuls (SNK)
Compare agora as diferenças
críticas pelos testes LSD de Fisher, DHS de Tukey e o S de
Scheffé (este para comparar duas médias, para permitir a comparação).
Tabela 4
Diferença crítica: testes LSD, HSD, Scheffé
1. Use o teste LSD não protegido se estiver
interessado em várias comparações individuais e não
estiver preocupado com múltiplas inferências.
2.
Para todas as comparações duas a duas, use o teste de Tukey.
3.
Para
comparações com um controle, use o teste de Dunnett.
📢 Algumas considerações
Imagine um ensaio com mais de dois grupos (se o número de grupos for dois, os testes darão o mesmo resultado) cujos resultados foram submetidos a uma análise de variância com um critério de classificação, no nível de significância de 5%.
🔸Se aplicar o teste de Tukey ou o teste de Dunnett, o nível de significância para experimentos será de 5%, mas o nível de significância para as comparações de médias será menor do que 5%.
🔸Se usar o teste LSD de Fisher (sem restrições), o teste de Duncan ou o teste de Newman Keuls, o nível de significância para comparações de médias será de aproximadamente 5%, mas o nível de significância para experimentos será maior ou muito maior (dependendo do número de tratamentos) do que 5%. Em compensação, o poder do teste será maior.
Escolha do Teste
🔺 Se quiser segurança para rejeitar H0, opte por Tukey, Dunnett ou LSD planejado — são
conservadores.
🔺Se quiser poder elevado, opte por LSD não-protegido
ou Duncan. O LSD é mais antigo, mais conhecido e de aplicação fácil.Também é
possível usar Tukey ou Dunnett com nível de significância mais alto. Por
exemplo, Tukey a 10% tem mais poder que Tukey a 5%.
A necessidade de aplicar um
teste que só rejeite a hipótese de que as médias são iguais com muita confiança
pode ocorrer quando se comparam novas drogas terapêuticas com uma droga
conhecida. Toda droga tem efeitos colaterais. Então, muitas vezes só é razoável
indicar uma nova droga – de efeitos colaterais desconhecidos – quando existem
indicações seguras de que essa nova droga é melhor do que a convencional.
Nos experimentos de competições
de marcas ou de variedades, ao contrário, muitas vezes é preciso um teste com
grande poder. Isto porque, nesses casos, o importante a alta probabilidade de
discriminação. O erro de rejeitar a hipótese de que duas marcas ou duas
variedades têm a mesma média – quando isso é verdade – tem importância menor.
✅ Considerações
Finais
O teste de Scheffé tem excelentes propriedades matemáticas, mas é excessivamente conservador. Já o teste de Bonferoni é indicado apenas quando o número pequeno de comparações de médias, pois se torna conservador quando o número de médias em comparação é grande.
Todos os testes têm vantagens e
desvantagens. Não existe um teste definitivamente “melhor” que todos os outros.
Os procedimentos para a comparação de médias não são exatos. No entanto, é
preciso adotar um procedimento formal para proceder à comparação de médias.
Isto evita que as conclusões fiquem totalmente dependentes da opinião do
pesquisador. De qualquer forma, existe uma grande margem de opção tanto na
escolha do teste, como no estabelecimento do nível de significância.
Dicas
Os cálculos foram feitos usando o software
SAS. Se você usar outro software ou fizer cálculos a mão pode ter pequenas
diferenças devido arredondamento. As diferenças serão provavelmente maiores
quando aplicar o teste SNK porque os valores são menos padronizados entre
tabelas.





No comments:
Post a Comment