PARADOXO DE SIMPSON: quando os dados enganam

 

Imagine que você quer verificar se, hoje em dia, as pessoas têm pouco conhecimento básico sobre história, geografia, ciências, matemática, religião, mas sabem muito sobre jogos no celular. Organiza então dois questionários sobre esses assuntos e seleciona, ao acaso, uma amostra de 300 pessoas ligadas a uma grande universidade, fossem elas alunos, funcionários ou professores, para se submeter a um teste.

Por facilidade, vamos chamar o questionário sobre conhecimentos gerais de A e o questionário sobre jogos de B. O questionário A foi respondido por 200 pessoas e o questionário B por 100. Os resultados da amostra foram claros: questões A foram respondidas corretamente por 80% da amostra e questões B por 50%. A conclusão foi a de que, na universidade, as pessoas têm mais conhecimento sobre assuntos gerais do que sobre jogos no celular. Os resultados obtidos estão na tabela abaixo.

Resultados da aplicação do questionário

Mas foi feita uma crítica: a amostra provavelmente teria muito mais jovens, que tendem a saber mais sobre jogos do que sobre assuntos gerais. E você resolveu, então, verificar. Separou a amostra de 300 pessoas em duas: a primeira constituída por pessoas com menos de 25 anos, que chamou de “Menos de 25” e a outra formada por pessoas com mais de 40 anos, que chamou de “Mais de 40”. Os jovens haviam respondido 190 questionários, 110 A e 80 B. Já as pessoas com mais de 40 haviam respondido 110 questionários, 38 A e 72 B. Veja estes resultados na tabela abaixo.

Resultados da aplicação do questionário

por faixa etária 

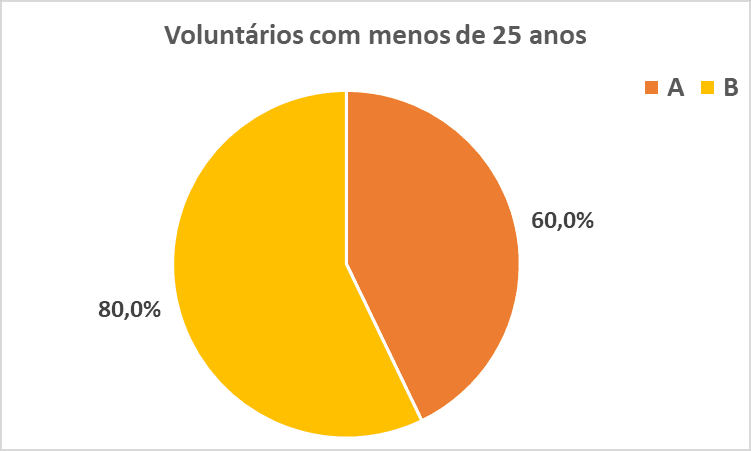
Agora o paradoxo se revela: no total, o questionário A mostrou melhores resultados. No entanto, quando observamos separadamente os grupos, de acordo com a faixa etária, vemos que a conclusão muda. Entre os jovens, o questionário B teve maior percentual de acertos; entre os mais velhos, o A teve um desempenho muito superior ao B. Essa inversão de conclusões ao se considerar ou ignorar uma variável de estratificação (a chamada variável de confusão ou de confundimento) é o que se conhece como Paradoxo de Simpson. Veja os gráficos.