Do My Data Need to Be Normally Distributed to Use ANOVA?

This is one of the most frequent questions asked by those starting to analyze data:

“Do my data need to be normally distributed?”

Let’s clarify:

To apply analysis of variance (ANOVA), it is not necessary for the data themselves to follow a normal distribution.

What is required is that the residuals (or errors) from the ANOVA model are approximately normally distributed.

🔍 What are residuals?

A residual is the difference between an observed value and the mean of the group it belongs to.

In a one-way ANOVA, the residual is calculated as:

                           Residual = observed value – group mean

📊 Example:

Imagine the data shown in Table 1. The group means are listed at the bottom of the table.

                                                         Table 1– Data from a trial

Based on these values, we calculate the residuals by subtracting the group mean from each data point.
                                                         Table 2 – Residuals

📈 Why analyze residuals?

The study of residuals — called residual analysis — is crucial because ANOVA assumes that residuals are normally distributed.

That’s why we always need to analyze the residuals when using ANOVA.

🧪 How do we analyze residuals?

A good practice is to examine residuals graphically and use statistical tests to verify that ANOVA assumptions are met. Figure 1 shows the histogram from Table 2 residuals.

                                          Figure 1. Histogram of residuals

Even if it’s not a “perfect normal distribution,” note the symmetry — this is a good sign. ANOVA is robust to minor violations of normality, especially when residuals are approximately symmetric. Figure 2 shows the boxplot of the residuals. 

Figure 2. Boxplot

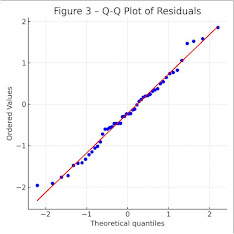
Symmetry and absence of outliers strengthen the case that ANOVA assumptions are satisfied. The Q-Q plot (quantile-quantile) compares observed residuals to what would be expected under normality. If points align along a 45° line, that’s a good sign. The P-P plot is another visual tool to assess normality.

                                                 Figure 3 – Q-Q plot of the residuals

                                       

📌 Descriptive statistics of residuals

  Some summary measures help evaluate the distribution:

■ Mean and median: If equal or close → symmetry
■ Skewness coefficient: Close to zero → good
■ Kurtosis: Negative values suggest a flatter distribution, which is not necessarily problematic

                     Table 3 – Descriptive statistics of residuals

                                    

In our example:
■ Mean = 0
■ Median = 0
· Skewness = 0 (symmetric)
· Slightly negative kurtosis (light tails), but still acceptable

✅ Statistical tests of normality

    Normality tests provide objective checks. The most common ones include:
              ■Shapiro-Wilk
              ■ Kolmogorov-Smirnov

In our example, the Kolmogorov-Smirnov test was performed in SPSS and resulted in p = 0.200.

That means there is no evidence to reject normality of the residuals.

⚠️ A note on sample size:

■ Small samples: less power to detect non-normality.
■ Large samples: may detect minor deviations that don't impact ANOVA results.

🧠 Final thoughts:

■ When group sizes are equal and fixed factors are used, ANOVA remains reliable despite slight violations of normality.
■ Problems arise mainly with high skewness or very different group variances.

💡 Important takeaway:

Raw data are usually not normally distributed, because they come from distinct groups expected to have different means.

What matters is:

➤ Whether the residuals follow a normal distribution, or
➤ Even better, whether each group’s data is normally distributed.

📚 References:

1. Ghasemi, A. & Zahediasl, S. (2012). Normality Tests for Statistical Analysis: A Guide for Non-Statisticians. Int J Endocrinol Metab. 10(2): 486–489.
2. Scheffé, H. (1959). The Analysis of Variance. Wiley.